CBSE
 Multiple Choice Questions
Multiple Choice Questions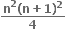 +n
+n
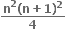
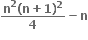
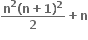
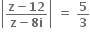 અને
અને 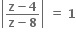 બંને શરતનું પાલન કરતી બધી સંકર સંખ્યાઓના કાલ્પનિક ભાગનો સરવાળો ....... થાય.
બંને શરતનું પાલન કરતી બધી સંકર સંખ્યાઓના કાલ્પનિક ભાગનો સરવાળો ....... થાય.35
28
25
28
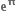

1
|z|
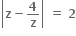 હોય, તો |z| નાં મહત્તમ તથા ન્યુનતમ મૂલ્યો વચ્ચેનો તફાવત ......... છે. (z≠0)
હોય, તો |z| નાં મહત્તમ તથા ન્યુનતમ મૂલ્યો વચ્ચેનો તફાવત ......... છે. (z≠0)
4
1
2
3


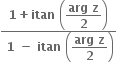
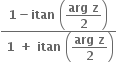
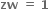


z = -w
B.

Tips: -
 ની પુન:ગોઠવણી કરતાં,
ની પુન:ગોઠવણી કરતાં, 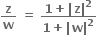 ... (1)
... (1)
∴ 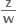 એ વાસ્તવિક સંખ્યા થશે. ધારો કે
એ વાસ્તવિક સંખ્યા થશે. ધારો કે 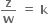 જ્યાં k ∈ R
જ્યાં k ∈ R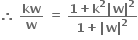 ((1)પરથી)
((1)પરથી) 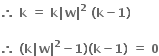
∴ k = 1 અથવા 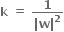
∴ 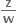 = 1 અથવા
= 1 અથવા 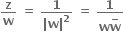

10
9
4
1
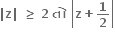 તો ની ન્યુનતમ કિંમત
તો ની ન્યુનતમ કિંમત
અંતરાલ (1, 2) માં છે,
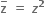 શરતનું પાલન કરતી કેટલી સંકર સંખ્યાઓ મળે ?
શરતનું પાલન કરતી કેટલી સંકર સંખ્યાઓ મળે ?
4
3
2
1