CBSE
 Multiple Choice Questions
Multiple Choice Questions1/2 ત્રિજ્યાવાળા વર્તુળ પર આવેલ છે.
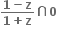
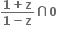
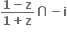

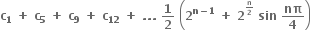

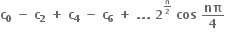
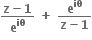 કાલ્પનિક ભાગ શુન્ય હોય, તથા
કાલ્પનિક ભાગ શુન્ય હોય, તથા 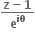 વાસ્તવિક ન હોય તો z એ
વાસ્તવિક ન હોય તો z એ
રેખા પર હોય.
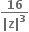 નું સમાધાન કરે તો |z|4 ની કિંમત ...... થાય.
નું સમાધાન કરે તો |z|4 ની કિંમત ...... થાય.1
2
3
4
 તો |z| ની ન્યુનતમ કિંમત ....... થાય.
તો |z| ની ન્યુનતમ કિંમત ....... થાય.




B.

Tips: -
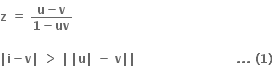

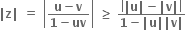

ઉપવલયની અંદરનો ભાગ
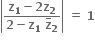 તથા |z2| ≠ 1. બિંદુ એ
તથા |z2| ≠ 1. બિંદુ એ
2 ત્રિજ્યાવાળા વર્તુળ પર હોય.
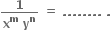
કાલ્પનિક અક્ષ પર હોય.
ઉપવલય પર હોય.
વર્તુળ પર હોય.
વાસ્તવિક અક્ષ પર હોય.