CBSE
 Multiple Choice Questions
Multiple Choice Questions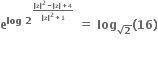 તો |z| = .......
તો |z| = .......

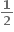
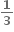
1
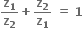 તો O(0), P(z1) તથા Q(z2) એ
તો O(0), P(z1) તથા Q(z2) એ
સમબાજુ ત્રિકોણ બનાવે.
રેખા પરનાં બિંદુઓ છે.
કાટકોણ ત્રિકોણનાં શિરોબિંદુઓ છે.
એકમ વર્તુળ પર આવેલ છે.
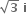 જો તો z2, z3 અનુક્રમે ........ થાય.
જો તો z2, z3 અનુક્રમે ........ થાય. 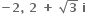
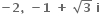
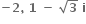

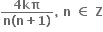
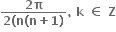
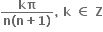
આપેલ પૈકી એક પણ નહી
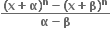 = ......
= ...... 



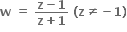 તો Re(w)
તો Re(w)
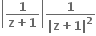
0
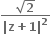
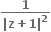
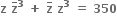 ના બીજથી રચાતા લંબચોરસનું ક્ષેત્રફળ ......
ના બીજથી રચાતા લંબચોરસનું ક્ષેત્રફળ ......68
175
350
48
 નાં શિરોબિંદુઓ છે. જો z0 એ
નાં શિરોબિંદુઓ છે. જો z0 એ  નું પરિકેન્દ્ર હોય, તો
નું પરિકેન્દ્ર હોય, તો 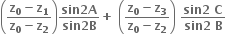
2
1
-1
0
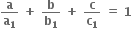 અને
અને 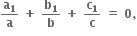 તો
તો 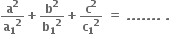
2 + 2i
2i
2
1 + 2i
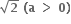 સમીકરણને કેટલા ઉકેલ મળે ?
સમીકરણને કેટલા ઉકેલ મળે ?
3
4
2
1
B.
4
Tips: -
ધારો કે z = reiθ
|z| = r = a 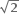 અને z2 = 2a2e2iθ
અને z2 = 2a2e2iθ
હવે, Re(z)2 = 2a2 cos 2 θ = 0
∴ 2θ = n
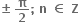
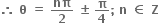
એક પ્રરિભ્રમણમાં 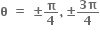
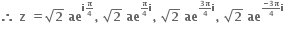
એમ ચાર ઉકેલ શક્ય બને.