Book Store

Download books and chapters from book store.
Currently only available for.
CBSE

Gujarati JEE Mathematics : ગણ, સંબંધ અને વિધેય

Multiple Choice Questions

11. જો f(x)= $square root of bold log bold space bold left parenthesis bold sin bold space bold x bold right parenthesis end root$ હોય, તો વિધેય f નો મહત્તમ પ્રદેશ ......... હોય.

$left curly bracket left parenthesis 4 straight k space plus space 3 space right parenthesis space straight pi over 2 vertical line space straight k space element of space straight Z right curly bracket$
$left curly bracket space left parenthesis 4 straight k space minus 1 right parenthesis space straight pi over 2 vertical line space straight k space element of space straight Z right curly bracket$
$left curly bracket left parenthesis 4 straight k space plus space 1 right parenthesis space straight pi over 2 vertical line space straight k element of straight Z right curly bracket space$
$left curly bracket left parenthesis 4 straight k space plus space 3 space right parenthesis space straight pi over 4 vertical line space straight k space element of space straight Z right curly bracket$

12.

જો $bold f bold left parenthesis bold x bold right parenthesis bold space bold equals bold space fraction numerator bold x bold minus bold 3 over denominator bold x bold plus bold 1 end fraction bold comma bold space bold x bold space bold not equal to bold space bold minus bold 1$ હોય તો f⁽²⁰¹⁶⁾(2015) = ...... જ્યાં f⁽²⁰¹⁶⁾(x) એ f નું f સાથે 2016 વખત સંયોજિત વિધેય દર્શાવે છે.

2017
2014
2016
2015

2015

Tips: -

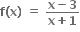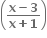
$bold f bold left parenthesis bold x bold right parenthesis bold space bold equals bold space fraction numerator bold x bold minus bold 3 over denominator bold x bold plus bold 1 end fraction$ આથી f(f(x)) = f $open parentheses fraction numerator bold x bold minus bold 3 over denominator bold x bold plus bold 1 end fraction close parentheses$

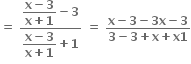
$bold equals bold space fraction numerator begin display style fraction numerator bold x bold minus bold 3 over denominator bold x bold plus bold 1 end fraction end style bold minus bold 3 over denominator begin display style fraction numerator bold x bold minus bold 3 over denominator bold x bold plus bold 1 end fraction end style bold plus bold 1 end fraction bold space bold equals bold space fraction numerator bold x bold minus bold 3 bold minus bold 3 bold x bold minus bold 3 over denominator bold 3 bold minus bold 3 bold plus bold x bold plus bold x bold 1 end fraction$
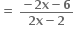
   f⁽²⁾(x) $bold equals bold space fraction numerator bold minus bold 2 bold x bold minus bold 6 over denominator bold 2 bold x bold minus bold 2 end fraction$

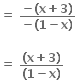
   $bold equals bold space fraction numerator bold minus bold left parenthesis bold x bold plus bold 3 bold right parenthesis over denominator bold minus bold left parenthesis bold 1 bold minus bold x bold right parenthesis end fraction bold equals bold space fraction numerator bold left parenthesis bold x bold plus bold 3 bold right parenthesis over denominator bold left parenthesis bold 1 bold minus bold x bold right parenthesis end fraction$

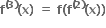
આ જ રીત, $bold f to the power of bold left parenthesis bold 3 bold right parenthesis end exponent bold left parenthesis bold x bold right parenthesis bold space bold equals bold space bold f bold left parenthesis bold f to the power of bold left parenthesis bold 2 bold right parenthesis end exponent bold left parenthesis bold x bold right parenthesis bold right parenthesis$

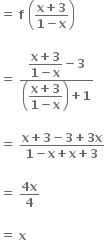
   $bold equals bold space bold f bold space open parentheses fraction numerator bold x bold plus bold 3 over denominator bold 1 bold minus bold x end fraction close parentheses bold equals bold space fraction numerator begin display style fraction numerator bold x bold plus bold 3 over denominator bold 1 bold minus bold x end fraction end style bold minus bold 3 over denominator open parentheses begin display style fraction numerator bold x bold plus bold 3 over denominator bold 1 bold minus bold x end fraction end style close parentheses bold plus bold 1 end fraction bold equals bold space fraction numerator bold x bold plus bold 3 bold minus bold 3 bold plus bold 3 bold x over denominator bold 1 bold minus bold x bold plus bold x bold plus bold 3 end fraction bold equals bold space fraction numerator bold 4 bold x over denominator bold 4 end fraction bold equals bold space bold x$

∴ f⁽⁴⁾(x) = f^(x); f⁽⁵⁾(x) = f⁽²⁾ (x) તથા f⁽⁶⁾ (x) = x મળે.

આમ, f^3k (x) = x;k ≥ 1, k ∈ N થાય.

∴f²⁰¹⁶ (x) = f^{3 (672)} (x) = x

∴ f²⁰¹⁶ (2015) = 2015

13. વાસ્તવિક વિધેય f(x) = $square root of bold x to the power of bold 2 bold space bold plus bold space bold 6 bold x bold space bold plus bold space bold 10 end root$ નો વિસ્તાર ...... મળે.

(-∞, 1)
[1, ∞]
R
(1, ∞)

14. જો f(x) = cos (log x) હોય, તો f(x), f(y) - $bold minus bold 1 over bold 2 bold space open square brackets bold f open parentheses bold x over bold y close parentheses bold plus bold f bold left parenthesis bold xy bold right parenthesis close square brackets bold space bold equals bold space bold. bold. bold. bold. bold space bold.$

15. f : (R -{-1} → R, f(x) = $fraction numerator bold 1 bold minus bold x over denominator bold 1 bold plus bold x end fraction$ હોય તો, $bold f bold space open parentheses fraction numerator bold x bold plus bold y over denominator bold 1 bold plus bold xy end fraction close parentheses$ = ..........

f(x) + f(y)
f(x)•f(y)
(f(x))²
f(x)/(f(y)

16.

જો f(x) એ દ્વિઘાત બહુપદી હોય તથા f(0) = 4 હોય તેમજ f(x+3) - f(x) 3x + 5, x હોય, તો તે દ્વિઘાત બહુપદી હોય.

3x² + x +24
x² + x + 24
$1 over 6$ (3x² + x + 24)
$1 half$ (x² + 2x + 9)

17. જો P = {1, 2, 3, 4,} Q = {a, b, c, d} હોય તો નીચેનાં જોડકાં જોડો :

i - c, ii - a, iii - b
i - b, ii - c, ii - a
i - a, ii - b, iii - c
i - a, ii - c, iii - b

18. જો X = {4ⁿ - 3n - 1, n ∈ N} અને Y = {9 (n-1); n ∈ N} જ્યાં N = પ્રાકૃતિક સંખ્યાઓનો ગણ હોય તો X ∪ Y = ......... .

X
Y - X
Y
N

19.

f(x) = ax² + bx + c; x = 1, 2, 3 તથા g(x) = $open curly brackets table attributes columnalign left end attributes row cell bold 3 bold x bold space bold plus bold 1 bold semicolon bold space bold x bold space bold equals bold space bold 2 bold comma bold 3 end cell row cell bold space bold space bold space bold space bold space bold space bold space bold space bold 3 bold semicolon bold space bold x bold space bold equals bold space bold 1 end cell end table close$ હોય તેમજ બંને વિધેયો સમાન હોય, તો નીચેનામાંથી કયું સત્ય બને ?

a = b = c = 1
$straight a space equals space minus 1 half comma space straight b space equals space 11 over 2 comma space straight c space equals space minus 2$
$straight a space equals 11 over 2 comma space straight b space equals space minus 2 comma space straight c space equals 1 half$
$straight a space equals space 1 half comma space straight b space equals space 2 comma space straight c space equals space 11 over 2$

20. જો વિધેય f એ સમીકરણ $bold 3 over bold 10 bold space bold f bold left parenthesis bold x bold right parenthesis bold space bold plus bold space bold 2 over bold 10 bold f bold space open parentheses fraction numerator bold x bold plus bold 59 over denominator bold x bold minus bold 1 end fraction close parentheses bold space bold equals bold space bold x bold space bold plus bold space bold 3$ નું સમાધાન કરે (જ્યાં $bold x bold space bold not equal to bold 1$ ) તો f(21) .......

Switch

Book Store

Subject

Gujarati JEE Mathematics : ગણ, સંબંધ અને વિધેય

Multiple Choice Questions

Switch