CBSE
 Multiple Choice Questions
Multiple Choice Questions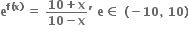 તથા f(x) = kf
તથા f(x) = kf 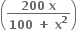 હોય, તો k = ...... .
હોય, તો k = ...... .
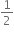
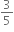

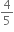
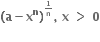 હોય, તો
હોય, તો 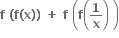 ............ મળે.
............ મળે. 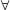 x > 0
x > 0
< 2
≥2
0≥0
=10
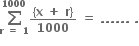
-x
x2
1/x
x
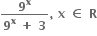 થી વિધેય વ્યાખ્યાયિત હોય, તો
થી વિધેય વ્યાખ્યાયિત હોય, તો
504
4032
2016
1008
 તથા f(g(x)) = xહોય, તો g
તથા f(g(x)) = xહોય, તો g 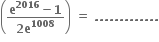
2016
252
1008
504
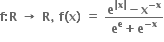
એક-એક અને વ્યાપ્ત વિધેય છે.
એક-એક વિધેય છે, પરંતુ વ્યાપ્ત વિધેય નથી.
એક-એક વિધેય નથી, પરંતુ વ્યાપ્ત વિધેય છે.
એક-એક પણ નથી તથા વ્યાપ્ત વિધેય નથી.
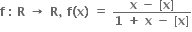 હોય, તો
હોય, તો 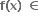 ...... જ્યાં [x] = પૂર્ણાંક ભાગ વિધેય.
...... જ્યાં [x] = પૂર્ણાંક ભાગ વિધેય.
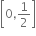
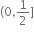
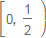
આપેલ પૈકી એક પણ નહી
{-1, 18}
{0}
{±2(3)}
0
 તથા g : [0, 2
તથા g : [0, 2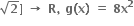 હોય, તો સંયોજિત વિધેય નો મહત્તમ પ્રદેશ ......તેમજ વિસ્તાર ......... મળે.
હોય, તો સંયોજિત વિધેય નો મહત્તમ પ્રદેશ ......તેમજ વિસ્તાર ......... મળે.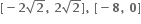
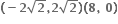
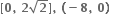
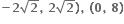
[1, ∞]
R+
R
[0, ∞]
D.
[0, ∞]
Tips: -
અહીં f(x) = 1 + x3, નો સહપ્રદેશ [1, ∞] છે.
એટલે કે, f(x) ≥ 1 છે. આથી 1 + x3 ≥ 1
∴ x3≥ 0 આથી x ≥ 0
∴ x ∈ [0, ∞] થાય.
હવે 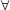 x1, x2 ∈ [ 0, ∞] માટે
x1, x2 ∈ [ 0, ∞] માટે
f(x1) = f(x2)
∴ x13 = x23 ⇒ x1 = x2
∴ f એક-એક વિધેય થાય.
આથી, x ∈ [0, ∞] હોય, તો f એક-એક વિધેય બને.