CBSE
 Multiple Choice Questions
Multiple Choice Questions
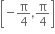
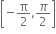
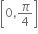
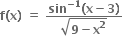 નો મહત્તમ પ્રદેશ ....... હોય.
નો મહત્તમ પ્રદેશ ....... હોય.
[3, 2]
[2, 1]
[2, 3)
[1, 2]
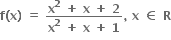 નો વિસ્તાર ....... હોય.
નો વિસ્તાર ....... હોય.
(1, ∞)
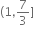
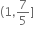
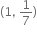
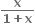 હોય, તો f એ ......... .
હોય, તો f એ ......... .
એક-એક તથા વ્યાપ્ત વિધેય છે.
એક-એક વિધેય નથી પરંતુ વ્યાપ્ત વિધેય છે.
એક-એક નથી તથા વ્યાપ્ત વિધેય પણ નથી
એક-એક વિધેય છે પરંતુ વ્યાપ્ત વિધેય નથી
D.
એક-એક વિધેય છે પરંતુ વ્યાપ્ત વિધેય નથી
Tips: -
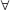 x1, x2 ∈ [0, ∞), f(x1) = f(x2) હોય, તો
x1, x2 ∈ [0, ∞), f(x1) = f(x2) હોય, તો 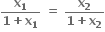
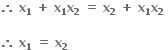
∴ f એક-એક વિધેય છે.
હવે, 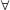 y, y ∈ [0, ∞),
y, y ∈ [0, ∞),  લેતાં
લેતાં
x = y + xy
∴ x - xy = y
∴x(1-y) = y આથી x = 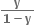 મળે. y = 1 હોય તો x અવ્યાખ્યાયિત બને.
મળે. y = 1 હોય તો x અવ્યાખ્યાયિત બને.
આથી y ≠ 1
f(x) = 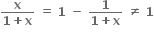
∴ Rf ≠[0, ∞)
∴ f વ્યાપ્ત વિધેય નથી.
f એક-એક વિધેય છે પરંતુ વ્યાપ્ત વિધેય નથી.
 )2 હોય, તો ......
)2 હોય, તો ......
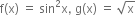
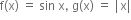
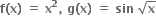
f અને g નિશ્વિત ન કરી શકાય.
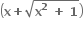 એ .........
એ .........
અયુગ્મ વિધેય છે.
યુગ્મ કે અયુગ્મ વિધેય નથી.
યુગ્મ વિધેય છે.
આવર્તી વિધેય છે.
સંમિત સંબંધ નથી
સ્વવાચક સંબંધ છે.
પરંપરિત સંબંધ છે.
કોઈ સંબંધ નથી.
1 +
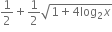
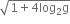
અસ્તિત્વ ધરાવતું નથી
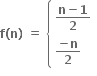
એક-એક નથી તથા વ્યાપ્ત વિધેય પણ નથી.
એક-એક વિધેય છે પરંતુ વ્યાપ્ત વિધેય નથી.
વ્યાપ્ત વિધેય છે પરંતુ એક-એક વિધેય નથી.
એક-એક તથા વ્યાપ્ત વિધેય છે.
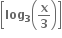 નો મહત્તમ પ્રદેશ ............ છે.
નો મહત્તમ પ્રદેશ ............ છે.
[1, 9]
(1, 9)
[9, 1]
[-1, 9]