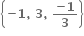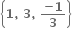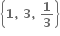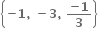CBSE
 Multiple Choice Questions
Multiple Choice Questions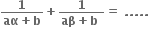

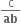
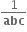
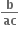
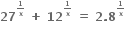 નાં વાસ્તવિક બીજોની સંખ્યા ....... છે.
નાં વાસ્તવિક બીજોની સંખ્યા ....... છે.
3
0
1
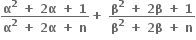 ની કિંમત ...... હોય.
ની કિંમત ...... હોય.
4
1
2
0
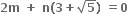
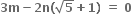
D.
x2 - 4x - 12 = 0Tips: -
ધારો કે માંગેલ દ્વિઘાત સમીકરણનાં બીજ α અને β છે.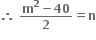 સમીકરણ m (40 - n) = 208 માં મૂકતાં,
સમીકરણ m (40 - n) = 208 માં મૂકતાં, 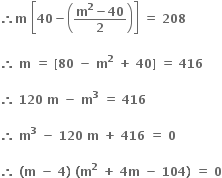
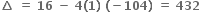
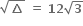 અસંમેય સંખ્યા છે. પરંતુ α, β સંમેય છે.
અસંમેય સંખ્યા છે. પરંતુ α, β સંમેય છે.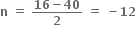
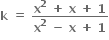 હોય તો k ∈ ....... .
હોય તો k ∈ ....... .
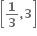
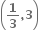
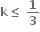
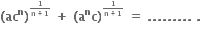
-ab
-b
-c
-a
-6, -1
-6, 1
-1, 6
6, 1
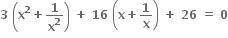 નો ઉકેલ ગણ ...... હોય.
નો ઉકેલ ગણ ...... હોય.