CBSE
 Multiple Choice Questions
Multiple Choice Questions3
2
1
0
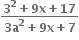 ની મહત્તમ કિંમત ........ હોય.
ની મહત્તમ કિંમત ........ હોય.
1
1/4
17/7
41
D.
41
Tips: -
ધારો કે,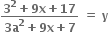
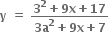 ની મહત્તમ કિંમત 41 હોય.
ની મહત્તમ કિંમત 41 હોય.
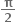 , હોય તથા સમીકરણ ax2 + bx + c = 0 (જ્યાં a ≠0)) નાં બીજ tan
, હોય તથા સમીકરણ ax2 + bx + c = 0 (જ્યાં a ≠0)) નાં બીજ tan  તથા
તથા  હોય, તો નીચેનામાંથી કયું સત્ય બને ?
હોય, તો નીચેનામાંથી કયું સત્ય બને ? 1 તથા 2 ની વચ્ચે