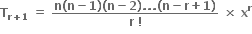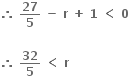CBSE
 Multiple Choice Questions
Multiple Choice Questions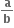
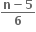
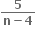


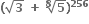 માં પૂર્ણાંક પદોની સંખ્યા ....... છે.
માં પૂર્ણાંક પદોની સંખ્યા ....... છે.
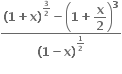 નું લગભગ મૂલ્ય ...... છે.
નું લગભગ મૂલ્ય ...... છે. 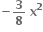
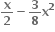
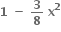
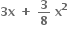
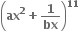 માં x7 નો સહગુણક અને
માં x7 નો સહગુણક અને 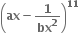 માં x-7 નો સહગુણક સમાન હોય, તો
માં x-7 નો સહગુણક સમાન હોય, તો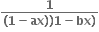 નું x ના ઘાતમાં વિસ્તરણ a0 + a1x + a2x3 + .... હોય, તો an = ..... .
નું x ના ઘાતમાં વિસ્તરણ a0 + a1x + a2x3 + .... હોય, તો an = ..... .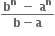
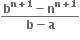
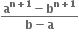
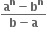
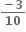
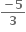
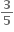
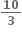
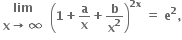 તો a અને b ની કિંમતો ....... છે.
તો a અને b ની કિંમતો ....... છે.
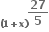 ના વિસ્તરણમાં પ્રથમ ઋણ પદ ......... છે.
ના વિસ્તરણમાં પ્રથમ ઋણ પદ ......... છે.
7 મું પદ
C.
8 મું પદTips: -