CBSE
 Multiple Choice Questions
Multiple Choice Questions0
3
5
8
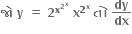 = ......
= ......

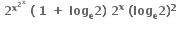

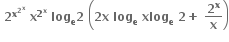
 = ........
= ........
4
3
2
1
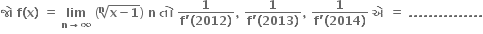
સ્વરિત શ્રેણિમાં હોય.
સમાંતર શ્રેણીમાં હોય.
સમગુણોત્તર શ્રેણીમાં હોય.
એક પણ નહિ.
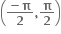 g(x) 2 tan-1 (ex)-
g(x) 2 tan-1 (ex)-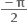 અને f એ g નું પ્રતિવિધેય હોય તો f'(0) = ........
અને f એ g નું પ્રતિવિધેય હોય તો f'(0) = ........ 4
3
2
1
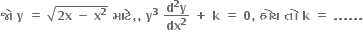
4
3
2
1
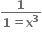 તો g(x) = .......
તો g(x) = ....... 1+[g(x)]3
1+ g(x)
g(x)
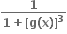
f એ વિકલનીય વિધેય છે તથા 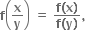 x#0, y#0, f(y) # 0 છે. જો f'(1) = 2 હોય તો f'(1) = 2 હોય તો f'(x) = .......
x#0, y#0, f(y) # 0 છે. જો f'(1) = 2 હોય તો f'(1) = 2 હોય તો f'(x) = .......
2x f(x)
2 f(x)
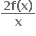

વિધેય f : R → R માટે નીચે આપેલ પૈકી કયા વિધન સત્ય (T) કે મિથ્યા (F) છે ?
(1) જો |f(x) - f(y)|≤30 |x - y|, ∀x, y, ∈ R, તો f એ R પર સતત વિધેય છે.
(2) જો |f(x) - f(y)|≤30 |x - y|, ∀x, y, ∈ R, તો f એ R પર વિકલનીય વિધેય છે.
(3) જો |f(x) - f(y)|≤21 |x - y|2, ∀x, y, ∈ R, તો f એ R પર વિકલનીય વિધેય છે.
(4) જો |f(x) - f(y)|≤21 |x - y|2, ∀x, y, ∈ R, તો f એ અચળ વિધેય છે.
TFTF
FTTF
TFTT
TTTT
C.
TFTT
Tips: -
વિધાન (1) સત્ય છે તે લક્ષની વ્યાખ્યા પરથી (δ = લો) સહેલાઈથી સાબિત કરી શકાય.
વિધાન (2) મિથ્યા છે, તે f(x) = |x| લઈને ચકાસી શકાય.
વિધાન (3), (4) માટે કોઈક a ∈ R માટે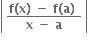 ≤ 21 |x - a|
≤ 21 |x - a|
∴ f એ R પર વિકલનીય વિધેય છે.
જો x→a તો |f(a)| ≤ 0
∴ |f'(a)| = 0
∴ f એ અચળ વિધેય છે. આથી વિધાન (3), (4) સત્ય છે.
h(x) એ સતત વિધેય તેમજ વિકલનીય વિધેય છે.
h(x) એ સતત વિધેય છે અને ફક્ત x = 0 આગળ વિકલનીય છે.
h(x) એ અસતત વિધેય છે.
h(x) એ સતત વિધેય છે પરંતુ x = 0 આગળ વિકલનીય નથી.