CBSE
 Multiple Choice Questions
Multiple Choice Questionsx + 2y = 4
2x + y = 2
2x + y = 0
2x + y = 4




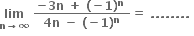
જો n અયુગ્મ સંખ્યા હોય તો 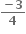
જો n યુગ્મ સંખ્યા હોય તો 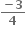
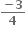
લક્ષનું અસ્તિત્વ નથી.
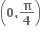 માં ઘટતું વિધેય છે.
માં ઘટતું વિધેય છે.
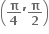 માં વધતું વિધેય છે.
માં વધતું વિધેય છે.
વિધેય g ને x = 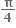 આગળ સ્થાનીય ન્યુનતમ મળે.
આગળ સ્થાનીય ન્યુનતમ મળે.
વિધેય g ને x = 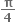 આગળ સ્થાનીય મહત્તમ મળે.
આગળ સ્થાનીય મહત્તમ મળે.
a < -3
-1 , a < 1
3 < a < 4
5 < a < 6
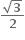 તો
તો 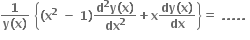
1
2
8
9
f'(1) = 0
2f(0) + f"(0) = 0
2f(0) + f"(0) = 2
f(2) = 0
7
8
10
0
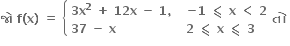
f ને x = 2 આગળ મહત્તમ કિંમત મળે.
f એ (10, 2) માં વધતું વિધેય છે.
f એ [-1, 3] પર સતત વિધેય છે.
f'(2)નું અસ્તિત્વ નથી.
A.
f ને x = 2 આગળ મહત્તમ કિંમત મળે.
B.
f એ (10, 2) માં વધતું વિધેય છે.
C.
f એ [-1, 3] પર સતત વિધેય છે.
D.
f'(2)નું અસ્તિત્વ નથી.
Tips: -
f એ બહુપદી વિધેય છે. 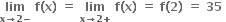
∴ f એ [-1. 3] થી સતત વિધેય છે. 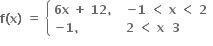
f'(2-) 24, f'(2+) = -1 આથી f'(2)નું અસ્તિત્વ નથી.
f'(x) = 6x + 12 = 6 (x + 2) > 0
∴ f એ (-1, 2) માં વધતું વિધેય છે.
વળી, f એ (2, 3) માં ઘટતું વિધેય છે.
∴ f ને x = 2 આગળ મહત્તમ કિંમત મળે.
n મહત્તમ તથા n ન્યુનત્તમ મૂલ્ય મળે.
મહત્તમ કે ન્યુનતમ મુલ્ય ન મળે.
ફક્ત એક મહત્તમ મૂલ્ય મળે.
ફક્ત એક ન્યુનતમ મૂલ્ય મળે.