CBSE
 Multiple Choice Questions
Multiple Choice Questions
A
0
A2
3
-3
9
27
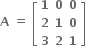 અને U1, U2, U3 એ એવા સ્તંભ શ્રેણિકો છે કે જેથી
અને U1, U2, U3 એ એવા સ્તંભ શ્રેણિકો છે કે જેથી 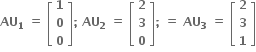 જો U એ 3×3 શ્રેણિક હોય કે જેના સ્તંંભ અનુક્રમે U1, U2, U3 છે તો |U| = ........
જો U એ 3×3 શ્રેણિક હોય કે જેના સ્તંંભ અનુક્રમે U1, U2, U3 છે તો |U| = ........ 3
-3
2
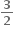
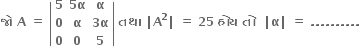
1
25
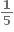
5
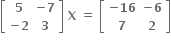 થાય તેવો 2×2 શ્રેણિક X = ........
થાય તેવો 2×2 શ્રેણિક X = ........
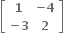
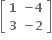
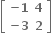
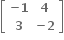
M અને N એ સંમિત અથવા વિસંમિત શ્રેણિકો હોય, તો અનુક્રમે NTMN એ સંમિત અથવા વિસંમિત શ્રેણિક છે.
MN - NM એ વિસંમિત શ્રેણિકો હોય, જ્યાં M અને N સંમિત શ્રેણિક છે.
જો M અને N એ સંમિત શ્રેણિકો હોય, તો MN એ સંમિત શ્રેણિક છે.
(adjM)(adjN) = adj(MN) જ્યાં M અને N સામાન્ય શ્રેણિકો છે.

-PT
-P
PT
P
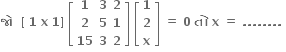
2, 14
2, 14
-2, 14
-2, -14
જો 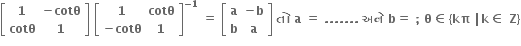
cos2θ, -sin2θ
-cos2θ, -sin2θ
-cos2θ, sin2θ
1,1
C.
-cos2θ, sin2θ
Tips: -
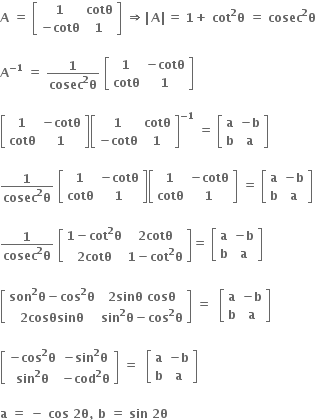
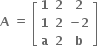 એ AAT = 91 નું સમાધાન કરે છે, તો ક્રમયુક્ત (a,b) = .......
એ AAT = 91 નું સમાધાન કરે છે, તો ક્રમયુક્ત (a,b) = ....... (2, 1)
(2, -1)
(-2, -1)
(-2, 1)