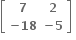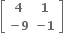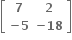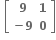CBSE
 Multiple Choice Questions
Multiple Choice Questions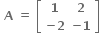 નો લંબ શ્રેણિક ....... થાય.
નો લંબ શ્રેણિક ....... થાય.
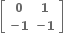
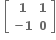


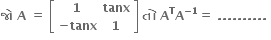
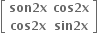
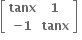
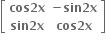
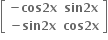
D.
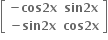
Tips: -
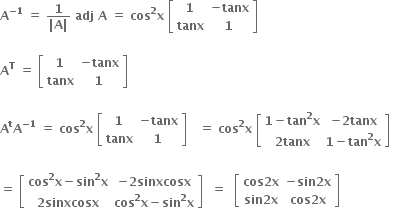
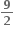
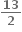
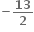
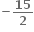
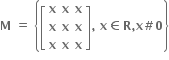 નો એકમ ઘટક ....... છે.
નો એકમ ઘટક ....... છે. 



1453
1435
4135
3135
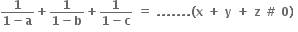
1
•2
-1
-2
જો a,b,c શુન્યેત્તર ધન વાસ્તવિક સંખ્યાઓ હોય, તો x, y, z ની સમીકરણ સંહતિ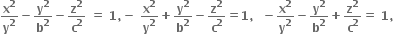
અનંત ઉકેલો છે.
એકથી વધુ સાન્ત ઉકેલો છે.
ઉકેલ નથી.
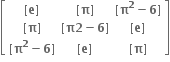
-8
8
1
0
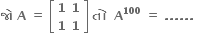
I
2100A
299A
2101A
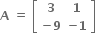 તો I + 2A + 3A2 + 4A3 + ........ ∞ = ..........
તો I + 2A + 3A2 + 4A3 + ........ ∞ = ..........