CBSE
 Multiple Choice Questions
Multiple Choice Questions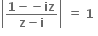 તો.......
તો.......
z એ શુદ્વ કાલ્પનિક સંખ્યા હોય.
P(z) એ બીજા ચરણમાં હોય.
P(z) એ ત્રીજા ચરણમાં હોય.
z એ વાસ્તવિક સંખ્યા હોય.
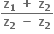 એ ...... છે.
એ ...... છે. 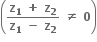
વાસ્તવિક અને ધન
શુદ્વ કાલ્પનિક સંખ્યા
વાસ્તવિક અને ઋણ
શૂન્ય સંખ્યા
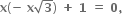 તો
તો 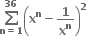 = ........... .
= ........... .
72
36
-72
0
 હોય અને બાકીનાં બે બીજનો ગુણાકાર 13 + i હોય, તો b = ......... .
હોય અને બાકીનાં બે બીજનો ગુણાકાર 13 + i હોય, તો b = ......... .
51
15
6
30
A.
51
Tips: -
આપેલ સમીકરણ x4 + ax3 + bx2 + cx + d = 0 છે. ... (1)
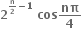
0
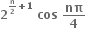
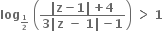 (જ્યાં
(જ્યાં 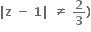 અસમતાનું પાલન કરતી સંકર સંખ્યાનો બિંદુગણ ......
અસમતાનું પાલન કરતી સંકર સંખ્યાનો બિંદુગણ ......વર્તુળનો બહારનો ભાગ.
વર્તુળ છે.
વર્તુળની અંદરનો ભાગ.
રેખા છે.
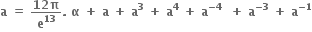 તથા
તથા 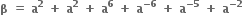 જેનાં બીજ હોય તેવું દ્વિઘાત સમીકરણ ......... છે.
જેનાં બીજ હોય તેવું દ્વિઘાત સમીકરણ ......... છે.x2 + x + 3 = 0
x2 - x + 2 = 0
x2 + x - 3 = 0
x3 - x - 3 = 0
x2 + x + 1 = 0
x2 + x - 1 = 0
x2 - x - 1 = 0
x2 - x + 1 = 0
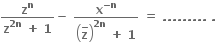
1
i
0
3
0
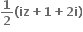
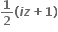
iz+1+i