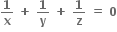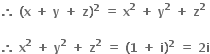CBSE
 Multiple Choice Questions
Multiple Choice Questions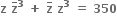 ના બીજથી રચાતા લંબચોરસનું ક્ષેત્રફળ ......
ના બીજથી રચાતા લંબચોરસનું ક્ષેત્રફળ ......68
175
350
48
 નાં શિરોબિંદુઓ છે. જો z0 એ
નાં શિરોબિંદુઓ છે. જો z0 એ  નું પરિકેન્દ્ર હોય, તો
નું પરિકેન્દ્ર હોય, તો 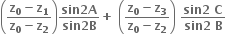
2
1
-1
0
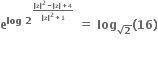 તો |z| = .......
તો |z| = .......

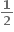
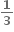
1
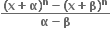 = ......
= ...... 



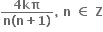
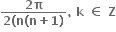
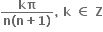
આપેલ પૈકી એક પણ નહી
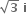 જો તો z2, z3 અનુક્રમે ........ થાય.
જો તો z2, z3 અનુક્રમે ........ થાય. 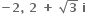
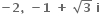
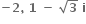

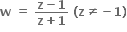 તો Re(w)
તો Re(w)
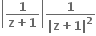
0
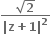
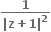
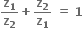 તો O(0), P(z1) તથા Q(z2) એ
તો O(0), P(z1) તથા Q(z2) એ
સમબાજુ ત્રિકોણ બનાવે.
રેખા પરનાં બિંદુઓ છે.
કાટકોણ ત્રિકોણનાં શિરોબિંદુઓ છે.
એકમ વર્તુળ પર આવેલ છે.
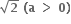 સમીકરણને કેટલા ઉકેલ મળે ?
સમીકરણને કેટલા ઉકેલ મળે ?
3
4
2
1
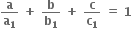 અને
અને 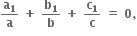 તો
તો 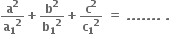
2 + 2i
2i
2
1 + 2i
B.
2i
Tips: -
ધારો કે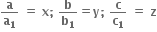 છે.
છે.