CBSE
 Multiple Choice Questions
Multiple Choice Questionsrα = rd = rp
rα = rd > rp
rα = rp < rd
rα < rp < rd
1 : 2
2 : 1


D.

 કોઈ એક છેડાથી અક્ષ પર અંતર x નો આલેખ ....... મળે.
કોઈ એક છેડાથી અક્ષ પર અંતર x નો આલેખ ....... મળે.

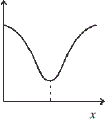
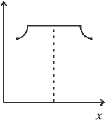

4.8 × 102
2.4 × 103
6 × 103
1.2 × 102


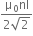

કુલંબનો નિયમ
ફેરેડેનો નિયમ
બાયો સાવરનો નિયમ
કિર્ચોફનો નિયમ


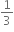

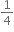
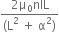
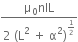
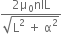
શુન્ય


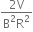


M2T A-2
M1T-2A-1
M1L-2A-1
M2LT2A-1