Book Store

Download books and chapters from book store.
Currently only available for.
CBSE

Gujarati JEE Mathematics : ક્રમચય અને સંચય

Multiple Choice Questions

31. અંકોના પુનરાવર્તન સિવાય ત્રણ અંકોની યુગ્મ સંખ્યાઓ કેટલી બને ?

360
320
348
328

32. જો m= _nC₂ તો _mC₂ = ......... .

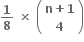
$bold 1 over bold 8 bold space bold cross times bold space open parentheses table row cell bold n bold plus bold 1 end cell row bold 4 end table close parentheses$
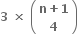
$bold 3 bold space bold cross times bold space open parentheses table row cell bold n bold plus bold 1 end cell row bold 4 end table close parentheses$
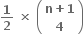
$bold 1 over bold 2 bold space bold cross times bold space open parentheses table row cell bold n bold plus bold 1 end cell row bold 4 end table close parentheses$
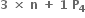
$bold 3 bold space bold cross times bold space bold n bold space bold plus bold space bold 1 bold space bold P subscript bold 4$

33.

ગણ {1, 2, 3, 4, ... n} ના 1 ને સમાવતા પરંતુ 2 ને ન સમાવતા ઓછામાં ઓછા 4 અને વધુમાં વધુ 5 ઘટકોવાળા ઉપગણોની સંખ્યા ..... છે. (n ≥ 6)

$open parentheses table row cell bold n bold minus bold 1 end cell row bold 4 end table close parentheses$
$open parentheses table row cell bold n bold minus bold 1 end cell row bold 5 end table close parentheses$
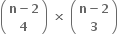
$open parentheses table row cell bold n bold minus bold 2 end cell row bold 4 end table close parentheses bold space bold cross times bold space open parentheses table row cell bold n bold minus bold 2 end cell row bold 3 end table close parentheses$
$open parentheses table row bold n row bold 5 end table close parentheses$

34. પ્રથમ n અયુગ્મ પ્રાકૃતિક સંખ્યાઓનો ગુણાકાર ....... છે.

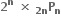
$bold 2 to the power of bold n bold space bold cross times bold space bold P presubscript bold 2 bold n end presubscript subscript bold n$
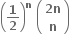
$open parentheses bold 1 over bold 2 close parentheses to the power of bold n bold space open parentheses table row cell bold 2 bold n end cell row bold n end table close parentheses$
n²
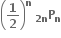
$open parentheses bold 1 over bold 2 close parentheses to the power of bold n bold space bold P presubscript bold 2 bold n end presubscript subscript bold n$

35.

એક સરકસમાં 10 પ્રાણીઓને રાખવા માટે 10 પાંજરાં છે. 3 પાંજરાં એટલાં નાનાં છે કે જેમા 10 પૈકી 6 પ્રાણી આવી શકે નહી. તો દરેક પાંજરામાં એક-એક પ્રાણી કેટલી રીતે ગોઠવી શકાય ?

30240
168
120960
5064

120960

Tips: -

7 પૈકી 6 મોટાં પાંજરામાં 6 મોટાં પ્રાણીઓને ગોઠવવાના પ્રકારની સંખ્યા = ₇P₆ = 7! = 7 × 720 = 5040

મોટા પાંજરામાં નાનું પ્રાણી આવી શકે.

∴ બાકીનાં 4 પાંજરામાં 4 પ્રાણીઓને ગોઠવવાના સંખ્યા = 4 ! = 24

∴ ગોઠવણીના કુલ પ્રકારની સંખ્યા = 5040 × 24 = 120960

36. 0, 1 અને 2 ની મદદથી 4 અંકોની કુલ કેટલી અયુગ્મ સંખ્યાઓ બને ?

37. 1, 2 અને 3 ની મદદથી જેના અંકોનો સરવાળો 10 થાય તેવી 7 અંકોની કેટલી સંખ્યાઓ બને ?

38. સંખ્યા 35679 ના અંકોની ફેરબદલી 56000 કરતાં નાની પાંચ આંકડાની નવી કેટલી સંખ્યાઓ બનાવી શકાય ?

143
29
28
30

39.

$bold square to the power of bold m bold space bold ABCD$ માં A - E - C અને B, E, D સમરેખ નથી. બિંદુઓ A, B, C, D, E ને આરંભ બિંદુ તરીકે લઈ કુલ ...... કિરણ દોરી શકાય.

40. બે B પાસપાસે ન આવે તે રીતે AAAA BB CCC DDD E F ને એક હારમાં કેટલી રીતે ગોઠવી શકાય ?

$fraction numerator bold 12 bold space bold factorial over denominator bold 4 bold space bold factorial bold space bold 3 bold space bold factorial bold space bold 3 bold space bold factorial end fraction bold space bold cross times bold space bold 13 to the power of bold 2$
$fraction numerator bold 12 bold space bold factorial over denominator bold 4 bold space bold factorial bold space bold 3 bold space bold factorial bold space bold 3 bold space bold factorial end fraction bold space bold cross times bold space open parentheses table row bold 13 row bold 2 end table close parentheses$
$fraction numerator bold 12 bold space bold factorial over denominator bold 4 bold space bold factorial bold space bold 3 bold space bold factorial bold space bold 3 bold space bold factorial end fraction bold space bold cross times bold space bold P presubscript bold 13 subscript bold 2$
$fraction numerator bold 14 bold space bold factorial over denominator bold 4 bold space bold factorial bold space bold 3 bold space bold factorial bold space bold 3 bold space bold factorial bold space bold 2 bold space bold factorial end fraction bold space bold minus bold space bold 2 bold factorial$

Switch

Book Store

Subject

Gujarati JEE Mathematics : ક્રમચય અને સંચય

Multiple Choice Questions

Switch