CBSE
 Multiple Choice Questions
Multiple Choice Questions વખત તો ગણિતીય અનુમાનના સિદ્વાંત પરથી કયું સત્ય છે?
વખત તો ગણિતીય અનુમાનના સિદ્વાંત પરથી કયું સત્ય છે?
 n ≥ 1
n ≥ 1
 n ≥ 1
n ≥ 1
 n ≥ 1
n ≥ 1
 n ≥ 1
n ≥ 1
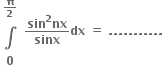
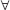 n ∈ N
n ∈ N
1
0
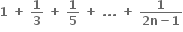
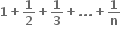
 અને I =
અને I = તો નીચેના પૈકી કયું દરેક n ≥ 1, n ∈ N માટે સત્ય છે ?
તો નીચેના પૈકી કયું દરેક n ≥ 1, n ∈ N માટે સત્ય છે ?
A.
An = 2n-1 A + (n-1)IB.
An = nA + (n+1) IC.
An = 2n-1 A - (n-1) ID.
An = nA - (n -1) IS(k) ⇒ S (k+1) સત્ય છે.