CBSE
 Multiple Choice Questions
Multiple Choice QuestionsS ને વ્યસ્ત સંબંધ ન હોય.
S એ એક-એક વિધેય નથી.
S વ્યાપ્ત વિધેય છે.
S એ વિધેય નથી.
સ્વવાચક સંબંધ ધરાવે પરંતુ સંમિત અને પરંપરિત નથી.
સ્વવાચક સંબંધ નથી પરંતુ સંમિત અને પરંપરિત છે.
સામ્ય સંબંધ છે.
સ્વવાચક અને સંમિત સંબંધ છે પરંતુ પરંપરિત સંબંધ નથી.
સંમિત તથા પરંપરિત છે.
સ્વવાચક અને સંમિત છે.
સ્વવાચક છે પરંતુ સંમિત કે પરંપરિત નથી.
સ્વવાચક તથા પરંપરિત છે.
સ્વવાચક અને સંમિત છે પરંતુ પરંપરિત નથી.
સામ્ય સંબંધ છે.
સ્વવાચક તથા પરંપરિત છે પરંતુ સંમિત નથી.
સંમિત તથા પરંપરિત છે પરંતું સ્વવાચક નથી.
S અને T માંથી કોઈ સામ્ય સંબંધ નથી.
T સામ્ય સંબંધ છે પરંતુ S સામ્ય નથી.
S અને T બંને સામ્ય સંબંધ છે.
S સામ્ય સંબંધ છે. પરંતુ T સામ્ય નથી.
219
211
220
256
સામ્ય સંબંધ છે.
માત્ર સ્વવાચક અને પરંપરિત સંબંધ છે.
માત્ર સ્વવાચક અને સંમિત સંબંધ છે.
માત્ર સ્વવાચક સંબંધ છે.
 હોય, તો નીચેનામાંથી કયું સત્ય બને ?
હોય, તો નીચેનામાંથી કયું સત્ય બને ?S તથા T સામ્ય સંબંધ નથી.
T સામ્ય સંબંધ છે. પરંતુ S સામ્ય સંબંધ નથી.
S અને T બંને સામ્ય સંબંધ છે.
S સામ્ય સંબંધ છે. પરંતુ T સામ્ય સંબંધ નથી.
B.
T સામ્ય સંબંધ છે. પરંતુ S સામ્ય સંબંધ નથી.
Tips: -
x = 0, y = 2, w = 0 લેતાં, 0 = 0 × 2 થાય.
ટુંકમાં, (0, 2) ∈ S મળે, પરંતુ (2, 0) ∉ S થાય. આથી S સંમિત નથી.
∴ S સામ્ય સંબંધ નથી.
હવે, nm = mn ⇒  આથી T સ્વવાચક છે.
આથી T સ્વવાચક છે.
mq = np ⇒ np = mq આથી T સંમિત છે.
આથી T સંમિત છે.
વળી, 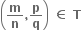 તથા
તથા 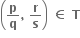 હોય, mq = np તથા sp = rq પરથી, nqsp = nprq
હોય, mq = np તથા sp = rq પરથી, nqsp = nprq
∴ ms = rn થાય. (pq, ≠ 0) (જો p = 0 તો m = r = 0)
∴ 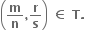 આથી T પરંપરિત છે.
આથી T પરંપરિત છે.
∴ T સામ્ય સંબંધ છે.
ટુંકમાં S સામ્ય સંબંધ નથી પરંતુ T સામ્ય સંબંધ છે.
સ્વવાચક તથા પરંપરિત છે પરંતુ સંમિત નથી.
સ્વવાચક છે પરંતુ સંમિત કે પરંપરિત નથી.
સંમિત તથા પરંપરિત છે પરંતુ સ્વવાચક નથી.
સામ્ય સંબંધ છે.
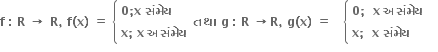 તો f-g
તો f-g
એક-એક વિધેય છે પરંતુ વ્યાપ્ત વિધેય નથી.
વ્યાપ્ત વિધય છે પરંતુ એક-એક વિધેય નથી.
એક-એક તથા વ્યાપ્ત વિધેય છે.
એક-એક નથી તથા વ્યાપ્ત વિધેય નથી.