CBSE
 Multiple Choice Questions
Multiple Choice Questions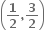
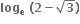
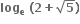
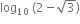
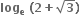
B.
a2 = b2 - 2acTips: -
અહી બે બીજનો સરવાળો, sin α + cos α = તથા બે બીજનો ગુણાકાર, sin α cos α
તથા બે બીજનો ગુણાકાર, sin α cos α 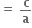 છે. ... (1)
છે. ... (1)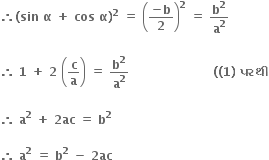
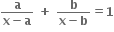 નાં બે બીજ એકબીજાની વિરોધી સંખ્યાઓ હોય તો 2(a+b) = .......
નાં બે બીજ એકબીજાની વિરોધી સંખ્યાઓ હોય તો 2(a+b) = .......
2
0
-1
1/2
± 4
± 3
± 2
± 1