Book Store

Download books and chapters from book store.
Currently only available for.
CBSE

Gujarati JEE Mathematics : દ્વિઘાત સમીકરણ

Multiple Choice Questions

41.

જો સમીકરણો x² + ax + b = 0 અને x² + bx + a = 0 નું એક બીજ સમાન હોય તો a + b ની કિંમત ......... હોય. (a ≠ b)

2
1
-1
0

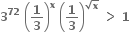42. x ∈ R માટે $bold 3 to the power of bold 72 bold space open parentheses bold 1 over bold 3 close parentheses to the power of bold x bold space open parentheses bold 1 over bold 3 close parentheses to the power of square root of bold x end exponent bold space bold greater than bold space bold 1$ હોય તો x ∈ ........ .

[0, 64]
(6, 64)
(0, 64]
[0, 64)

43.

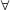x ∈ R માટે જો દ્વિઘાત બહુપદી f(x) = ax² + bx + c > 0 હોય તો g(x) = f(x) + f'(x) + f"(x) ....... થાય. x ∈ R.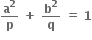

g(x) = 0
g(x) < 0
g(x) ≥0
g(x) > 0

44.

જો ax + by = 1 હોય અને સમીકરણ px² + qy² = 1 ને માત્ર એક જ બીજ હોય તો નીચેનામાંથી કયું સત્ય બને ?

a²b² = pq
$bold a to the power of bold 2 over bold p bold space bold plus bold space bold b to the power of bold 2 over bold q bold space bold equals bold space bold 1$
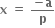
$bold x bold space bold equals bold space fraction numerator bold minus bold a over denominator bold p end fraction$
આપેલ પૈકી એક પણ નહી

45.

જો દ્વિઘાત સમીકરણ (x - a) (x - b) - k = 0 નાં બીજ c તથા d હોય તો a તથા b બીજવાળું દ્વિઘાત સમીકરણ ....... મળે.

(x - c) (x - d) + k = 0
(x + c) (x + d) - k = 0
(x - c) (x - d) - k = 0
(x + c) (x + d) + k = 0

46.

સમીકરણ (x - a) (x- b) + (x - b) (x - c) + (x - c) (x - a) = 0 નાં બીજ હંમેશાં ........ હોય. (a≠b)

વાસ્ત્વવિક અસમાન
સમાન
અવાસ્તવિક સંકર
શુદ્વ કાલ્પનિક

47.

a, b, c ∈ R; a ≠ 0 માટે જો સમીકરણ a²x² + bx + c = 0 નું એક બીજ α હોય તથા સમીકરણ a² x² - bx - c = 0 નું એક બીજ β હોય જ્યાં 0 < α < β હોય તો સમીકરણ a²x² + 2bx + 2c = 0 નું બીજ γ હંમેશા નીચેનામાંથી ........ નું સમાધાન કરે.

$bold alpha bold space bold less than bold space bold gamma bold space bold less than bold space bold beta$
$bold gamma bold space bold equals bold space bold alpha bold space bold plus bold space bold beta over bold 2$
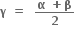
$bold gamma bold space bold equals bold space bold space fraction numerator bold alpha bold space bold plus bold beta over denominator bold 2 end fraction$
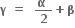
$bold gamma bold space bold equals bold space bold space fraction numerator bold alpha bold space over denominator bold 2 end fraction bold plus bold beta$

bold alpha bold space bold less than bold space bold gamma bold space bold less than bold space bold beta

Tips: -

સમીકરણ a²x² + bx + c = 0 નું એક બીજ α હોવાથી, a²^2α + bα + c = 0

∴ bα + c = -a²α² (1)

વળી, સમીકરણ a²x² - bx - c = 0 નું એક બીજ β હોવાથી, a²β² - bβ - c = 0

∴ bβ + c = a²β²

હવે, f(x) = a²x² + 2bx + 2c નું શુન્ય γ હોય તો, f(γ) = a²γ² + 2bγ + 2c = 0

∴ f(x) = a²x² + 2bx + 2c માં x = α લેતાં,

∴ f(α) = a²α² + 2bα + 2c

= a²α² + 2(bα + c) = a² α² - 2a² α² = -a²α²< 0 (1) પરથી,

વળી, f(x) = a²x² + 2bx + 2c માં x = β લેતાં,

∴ f(β) = a²β² + 2bβ + 2c

= a²β² + 2(bβ + c) = a²β² + 2a²β² = 3a²β² > 0 (2) પરથી,

f(α) <0 તથા f(β) > 0 હોવાથી, γ ∈ (α, β) એવો મળે કે જેથી f(γ) = 0 થાય.

∴ α < γ < β સત્ય બને.

48.

$bold log subscript bold 10 bold space bold a bold space bold plus bold space bold log subscript bold 10 bold space square root of bold a bold space bold plus bold space bold log subscript bold 10 bold space scriptbase square root of bold a end scriptbase presuperscript bold 4 bold space bold plus bold space bold. bold. bold. 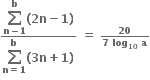bold space bold equals bold space bold b bold space bold greater than bold space bold 0$ હોય તથા $fraction numerator begin display style bold sum from bold n bold minus bold 1 to bold b of end style bold left parenthesis bold 2 bold n bold minus bold 1 bold right parenthesis over denominator begin display style bold sum from bold n bold equals bold 1 to bold b of end style bold left parenthesis bold 3 bold n bold plus bold 1 bold right parenthesis end fraction bold space bold equals bold space begin inline style fraction numerator bold 20 over denominator bold 7 bold space bold log subscript bold 10 bold space bold a end fraction end style$ હોય તો a = ...... .

1000
100
100000
10

49.

જો α, β એ સમીકરણ x² + px + q = 0 નાં બીજ હોય અને α⁴, β⁴ એ સમીકરણ x² - rx + s = 0 નાં બીજ હોય તો સમીકરણ x² - 4qx + 2q² - r = 0 નાં બીજ હંમેશાં ........ હોય.

બે સમાન અને વાસ્તવિક
બે ભિન્ન અને વાસ્તવિક
અવાસ્તવિક સંકર
એક વાસ્તવિક અને એક શુદ્વ કાલ્પનિક

50. ચલ x માં દ્વિઘાત સમીકરણ (cos p - 1)x² + cos px + sin p = 0 નાં બીજ વાસ્તવિક હોય તો, p ∈ .....

$bold left parenthesis bold 0 bold comma bold space bold 2 bold pi bold right parenthesis$
$bold left parenthesis bold minus bold pi bold comma bold space bold 0 bold right parenthesis$
$bold left parenthesis bold 0 bold comma bold space bold pi bold right square bracket$
$open parentheses fraction numerator bold minus bold pi over denominator bold 2 end fraction bold comma bold pi over bold 2 close parentheses$

Switch

Book Store

Subject

Gujarati JEE Mathematics : દ્વિઘાત સમીકરણ

Multiple Choice Questions

Switch