CBSE
 Multiple Choice Questions
Multiple Choice Questions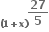 ના વિસ્તરણમાં પ્રથમ ઋણ પદ ......... છે.
ના વિસ્તરણમાં પ્રથમ ઋણ પદ ......... છે.
7 મું પદ
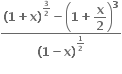 નું લગભગ મૂલ્ય ...... છે.
નું લગભગ મૂલ્ય ...... છે. 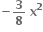
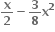
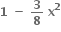
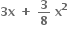
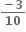
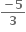
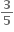
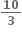
A.
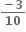
Tips: -
(1 + αx)4 ના વિસ્તરણમાં મધ્યમ પદનો સહગુણક = (1 -αx6) ના વિસ્તરણમાં મધ્યમ પદનો સહગુણક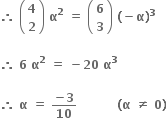
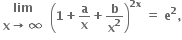 તો a અને b ની કિંમતો ....... છે.
તો a અને b ની કિંમતો ....... છે.
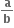
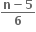
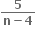


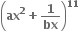 માં x7 નો સહગુણક અને
માં x7 નો સહગુણક અને 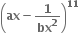 માં x-7 નો સહગુણક સમાન હોય, તો
માં x-7 નો સહગુણક સમાન હોય, તો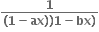 નું x ના ઘાતમાં વિસ્તરણ a0 + a1x + a2x3 + .... હોય, તો an = ..... .
નું x ના ઘાતમાં વિસ્તરણ a0 + a1x + a2x3 + .... હોય, તો an = ..... .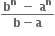
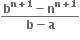
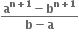
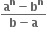
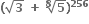 માં પૂર્ણાંક પદોની સંખ્યા ....... છે.
માં પૂર્ણાંક પદોની સંખ્યા ....... છે.