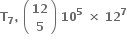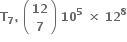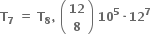CBSE
 Multiple Choice Questions
Multiple Choice Questions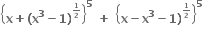 એ x માં ...... ઘાતની બહુપદી છે.
એ x માં ...... ઘાતની બહુપદી છે.
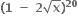 ના દ્વિપદી વિસ્તરણમાં x ના પૂર્ણાંક ઘાતાંકવાળાં પદોના સહગુણકોનો સરવાળો ....... છે.
ના દ્વિપદી વિસ્તરણમાં x ના પૂર્ણાંક ઘાતાંકવાળાં પદોના સહગુણકોનો સરવાળો ....... છે.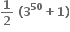
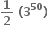
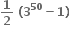
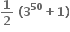
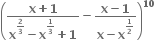 ના વિસ્તરણમાં અચળ પદ ..... છે.
ના વિસ્તરણમાં અચળ પદ ..... છે.
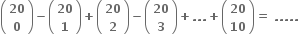
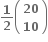

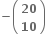
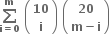 મહત્તમ છે. (જ્યાં જો p < q તો
મહત્તમ છે. (જ્યાં જો p < q તો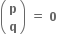 )
) 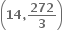
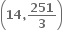
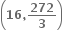
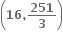
 ....... છે.
....... છે.
એક અયુગ્મ ધન પૂર્ણાંક
C.
એક અસંમેય સંખ્યાTips: -
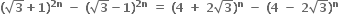
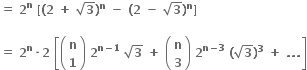
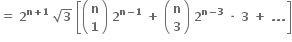 એક અસંમેય સંખ્યા છે.
એક અસંમેય સંખ્યા છે.