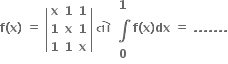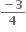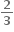CBSE
 Multiple Choice Questions
Multiple Choice Questionsજો a,b,c એ સ્વરિત શ્રેણીના અનુક્રમે p માં, r માં પદ હોય તો 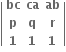 નું મુલ્ય ..... છે.
નું મુલ્ય ..... છે.
0
pqr
abc
એક પણ નહિ
જો 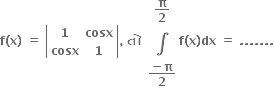
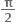

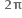
2
સમીકરણો (x + 1)x + 8y = 4k અને kx + (k + 3)y = 3k - 1 નો ઉકેલ મળે નહિ, તો k = ......
k ∈ R
1
2
3
D.
3
Tips: -
(k + 1)x + 8y - 4k = 0
kx + (x + 3)y - 3k + 1 = 0 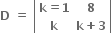 = K2 + 4K + 3 - 8K = K2 - 4K + 3 = (K - 3)(K - 1) = 0⇒k = 3 અથવા k = 1
= K2 + 4K + 3 - 8K = K2 - 4K + 3 = (K - 3)(K - 1) = 0⇒k = 3 અથવા k = 1 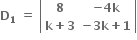 = -24 k+ 8 + 4k2 + 12 k
= -24 k+ 8 + 4k2 + 12 k
= 4k2 - 12k + 8 = 4(k - 2)(k - 1). k = 3 માટે D1 # 0, k = 1 માટે D1 = 0
k = 1 માટે ઉકેલ અનંતગણ, k = 2 માટે અનન્ય ઉકેલ.
k = 3 માટે સમીકરણો x + 2y = 3 તથા x + 2y = નો ઉકેલગણ છે. આથી k = 3
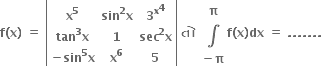
0
1
2
-2
જો y = -9 એ આપેલ સમીકરણનું એક બીજ છે, તો  નાં બીજાં બીજ ........ છે.
નાં બીજાં બીજ ........ છે.
-2 અને 7
2 અને 7
-2 અને -7
2 અને -7
જો 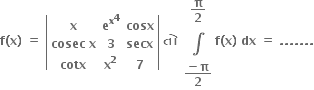
0
34


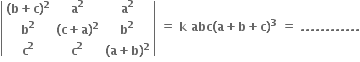
-1
1
-2
2
જો α, β અને γ એ સમીકરણ x3 + px + q = 0 નાં બીજ હોય, તો નું મૂલ્ય .......... છે.
3pq
p2 = 2q
p + q
p - q
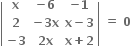
3 અથવા 2 અથવા 1
-3 અથવા 2 અથવા 1
-3 અથવા - 2 અથવા 1
-3 અથવા 2 અથવા -1