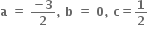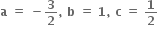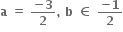CBSE
 Multiple Choice Questions
Multiple Choice Questions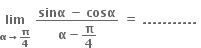
0
1
2
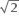
D.
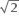
Tips: -
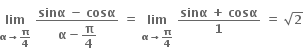
 = f(x) + f
= f(x) + f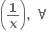 x ∈ Df અને f(1) > તો
x ∈ Df અને f(1) > તો  f(x) = .......
f(x) = .......1
2
3
લક્ષ્યનું અસ્તિત્વ નથી.
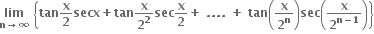
0
tan x
cot x
sec x
1
3
9
27
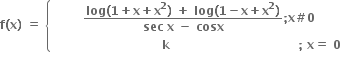 જો વિધેય f એ x = 0 આગળ સતત હોય, તો k = ..........
જો વિધેય f એ x = 0 આગળ સતત હોય, તો k = .......... 0
-1
1
2
 ની કઈ કિંમત માટે
ની કઈ કિંમત માટે 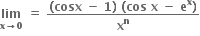 સાન્ત શુન્યેત્તર સંખ્યા મળે ?
સાન્ત શુન્યેત્તર સંખ્યા મળે ?
1
2
3
4
જો 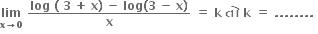
0
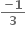
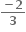
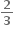
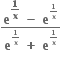 જ્યાં, g સતત વિધેય છે. જો
જ્યાં, g સતત વિધેય છે. જો  f(x) નું અસ્તિત્વ હોય, તો
f(x) નું અસ્તિત્વ હોય, તો g(x) = xh(x) જ્યાં h(x) બહુપદી વિધેય
g(x) એ અચળ વિધેય છે.
g(x) = x + 2
g(x) = x2 + 4
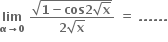

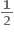
1
લક્ષનું અસ્તિત્વ નથી.
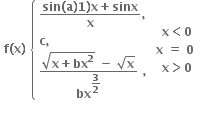 એ x = 0 આગળ સતત હોય તો ........
એ x = 0 આગળ સતત હોય તો ........