CBSE
 Multiple Choice Questions
Multiple Choice Questionsf(x) = (x2 - 3x + 2) |x - 1|
f(x) = |2x - 1|
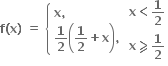
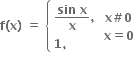
0< x <  હોય તેવું બીજ મળે.
હોય તેવું બીજ મળે.
 < x < 2 હોય તેવું બીજ મળે.
< x < 2 હોય તેવું બીજ મળે.
ઓછામાં ઓછું એક વાસ્તવિક બીજ મળે.
એક પણ બીજ પણ ના મળે.
C.
ઓછામાં ઓછું એક વાસ્તવિક બીજ મળે.
Tips: -
ધારો કે, f(x) = e-x - sin x અને α, β (α < β) એ f(x) નાં બે શૂન્ય છે. f(x) એ [α, β] પર સતત અને વિકલનીય છે તથા f(α) = f(β) = 0
રોલના પ્રમેય પરથી ઓછામાં ઓછો એક k ∈(α, β ) મળે કે જેથી f(k) = 0 થાય.
∴ f'(x) = -e-x - cos x
f'(x) = 0 ⇒ - e-k -cos k = 0 ⇒ -e-k (1 + ek cos k) = 0 ⇒ ek cos k = - 1
∴ k એ ex cos x = - 1 નું બીજ થાય.
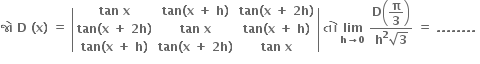
108
138
144
168
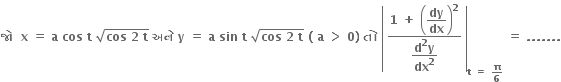
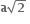
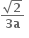
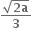
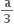
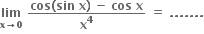
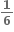
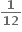
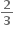
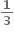
1
2
n
એક પણ નહિ.
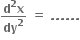
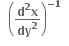
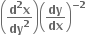
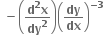
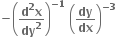
એક વસ્તવિક અને એક સંકર બીજ મળે.
એક પણ બીજ ન મળે.
બે અવાસ્તવિક સંકર બીજ મળે.
ઓછામાં ઓછું એક વાસ્તવિક બીજ મળે.
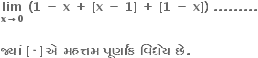
-1
1
0
લક્ષનું અસ્તિત્વ નથી.

0
અવિભાજ્ય સંખ્યા
અયુગ્મ વિભાજ્ય સંખ્યા
અસંમેય સંખ્યા