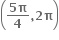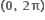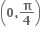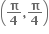CBSE
 Multiple Choice Questions
Multiple Choice Questions(b - c) f(a) + (c - b) f(b) > (c - a) f(c)
(b - a) f(c) + (c - b) f(a) > (c - a) f(b)
(b - a) f(c) + (c - b) f(a) < (c - a) f(b)
(b - c) f(a) + (c - b) f(b) > (c - a) f(c)
વિધેય f : (0, ∞) → (0, ∞) માટે,
(1) f(ab) = f(a) f(b) અને
(2)  f(x) = c, (જ્યાં ક # 0) પ્રકારનું છે. f(4) = ....
f(x) = c, (જ્યાં ક # 0) પ્રકારનું છે. f(4) = ....
1
2
3
4
FTFT
TTFF
TFTT
FTTF
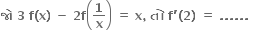
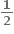
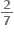
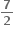
2
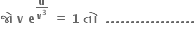
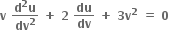
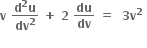
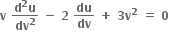
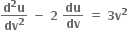
q




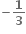

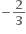

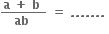
0
1
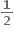
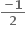
C.
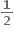
Tips: -
xy + ax + by = 0 નું વિકલન કરતાં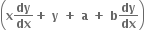 = 0
= 0 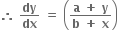
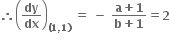 (આપેલ છે કે સ્પર્શક X-અક્ષ સાથે tan-1 2 માપનો ખૂણો બનાવે છે.)
(આપેલ છે કે સ્પર્શક X-અક્ષ સાથે tan-1 2 માપનો ખૂણો બનાવે છે.)
∴ a + 2b = -3 (1)
વળી, (1, 1) એ વક્ર પરનું બિંદુ છે. આથી 1 + a + b = 0. આથી a + b = -1 (2)
(1) અને (2) ને ઉકેલતાં, a = 1, b = -2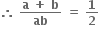
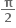

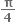

f(x) = sin x + cos x, 0 ≤ x ≤ 2 એ ...... અંતરાલમાં ચુસ્ત ઘટતું વિધેય છે.
એ ...... અંતરાલમાં ચુસ્ત ઘટતું વિધેય છે.