CBSE
 Multiple Choice Questions
Multiple Choice Questions(0, 2)
(0, -2)
(0, 1)
(0, -1)
2
-3
4
5
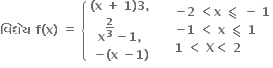
1
2
3
4
નીચેનામાંથી કયા અંતરાલમાં a ની કિંમત આવે તો
f(x) = sinx - asin2x -  sinx3 + 2ax એ R પર વધતું વિધેય થાય ?
sinx3 + 2ax એ R પર વધતું વિધેય થાય ?
[0, ∞)
[1, ∞)
[0, ∞)
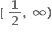
જો f(x)= અને g(x) = , 0<x<1, તો આ અંતરાલમાં
f(x) વધતું વિધેય છે અને g(x) ઘટતું વિધેય છે.
g(x) વધતું વિધેય છે અને f(x) ઘટતું વિધેય છે.
f(x) અને g(x) બંને વધતાં વિધેય છે.
f(x) અને g(x) બંને ઘટતાં વિધેય છે.
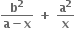 , 0 < x < a નું ન્યુનતમ મૂલ્ય ...... થાય.
, 0 < x < a નું ન્યુનતમ મૂલ્ય ...... થાય. 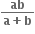
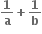
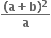
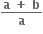
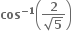
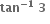
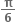
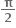
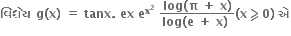
 પર વધતું તથા
પર વધતું તથા 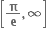 પર ઘટતું વિધેય છે.
પર ઘટતું વિધેય છે.
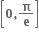 પર ઘટતું તથા
પર ઘટતું તથા 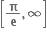 પર વધતું વિધેય છે.
પર વધતું વિધેય છે.
[0, ∞]પર વધતું વિધેય છે.
[0, ∞]પર ઘટતું વિધેય છે.
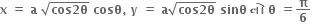 આગળનો સ્પર્શક .........
આગળનો સ્પર્શક ......... રેખા y = x ને સમાંતર છે.
રેખા x + y = 1 ને સમાંતર છે.
X-અક્ષને સમાંતર છે.
Y-અક્ષને સમાંતર છે.
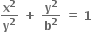 પર P કોઈ એક બિંદુ છે. કેન્દ્ર 0 માંથી દોરેલ P પરના સ્પર્શક પર દોરેલ લંબનો લંબપાદ N છે. ધારો કે Amax એ ∆OPN નું મહત્તમ ક્ષેત્રફળ છે.
પર P કોઈ એક બિંદુ છે. કેન્દ્ર 0 માંથી દોરેલ P પરના સ્પર્શક પર દોરેલ લંબનો લંબપાદ N છે. ધારો કે Amax એ ∆OPN નું મહત્તમ ક્ષેત્રફળ છે. 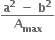 ની કિંમત .....
ની કિંમત ..... 1
2
4
8
C.
4
Tips: -
બિંદુ P ના યામ (acosθ, bsinθ) લો. 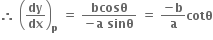
P બિંદુએ સ્પર્શકનું સમીકરણ
bxcosθ + aysinθ = ab
કાટકોણ ∆OPNમાં
PN2 - OP2 - ON2 
A ને મહત્તમ થવા માટે, f(0) = a2tanθ + b2cotθ ન્યુનત્તમ થાય.  = a2sec2-b2cosec2θ, f(θ) = 2b2cosec2a cotθ
= a2sec2-b2cosec2θ, f(θ) = 2b2cosec2a cotθ  0 ⇒ tanθ = ±
0 ⇒ tanθ = ± 
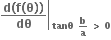
f(θ) એ tanθ =  હોય ત્યારે ન્યુનત્તમ થાય. અથી ન્યુનત્તમ f(θ) =
હોય ત્યારે ન્યુનત્તમ થાય. અથી ન્યુનત્તમ f(θ) =