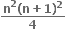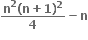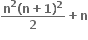CBSE
 Multiple Choice Questions
Multiple Choice Questions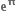

1
|z|
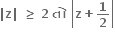 તો ની ન્યુનતમ કિંમત
તો ની ન્યુનતમ કિંમત
અંતરાલ (1, 2) માં છે,
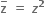 શરતનું પાલન કરતી કેટલી સંકર સંખ્યાઓ મળે ?
શરતનું પાલન કરતી કેટલી સંકર સંખ્યાઓ મળે ?
4
3
2
1
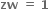


z = -w
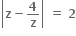 હોય, તો |z| નાં મહત્તમ તથા ન્યુનતમ મૂલ્યો વચ્ચેનો તફાવત ......... છે. (z≠0)
હોય, તો |z| નાં મહત્તમ તથા ન્યુનતમ મૂલ્યો વચ્ચેનો તફાવત ......... છે. (z≠0)
4
1
2
3


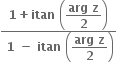
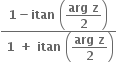
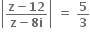 અને
અને 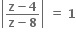 બંને શરતનું પાલન કરતી બધી સંકર સંખ્યાઓના કાલ્પનિક ભાગનો સરવાળો ....... થાય.
બંને શરતનું પાલન કરતી બધી સંકર સંખ્યાઓના કાલ્પનિક ભાગનો સરવાળો ....... થાય.35
28
25
28
C.
25
Tips: -
સહેલાઇથી જોઈ શકાય છે કે પ્રથમ સમીકરણ વર્તુળ દર્શાવે છે.
બીજું સમીકરણ એ (4, 0) તથા (8, 0) નો લંબદ્વિભાજક દર્શાવે છે.
∴ z નું સ્વરૂપ 6 + yi પ્રકારનું હોય.
∴ y = 8 અથવા y = 17
∴ z = 6 + 8i અથવા 6 + 7i
∴ માંગેલ સરવાળો = 8 + 17 = 25
10
9
4
1
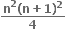 +n
+n