CBSE
 Multiple Choice Questions
Multiple Choice Questions3
0
-3
1
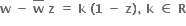 ના બિંદુગણનું સવરૂપ ....... થશે.
ના બિંદુગણનું સવરૂપ ....... થશે. {z | |z| = 1, z ≠1 }
{z | |z| = 1 }
{z |z = z }
{z | z ≠ 1}
f(x) = 0 ને એક ઋણ વાસ્તવિક બીજ મળે.
A.
f(x) = 0 ને એક ઋણ વાસ્તવિક બીજ મળે.
Tips: -
az2 + z + 1 = 0 જ્યાં a = cosθ + i sin θ
ધારો કે શુદ્વ કાલ્પનિક સંખ્યા z1 અને z2 એ આ સમીકરણનાં બીજ છે. 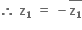 અને
અને 
બંને બીજનો સરવાળો 
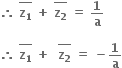
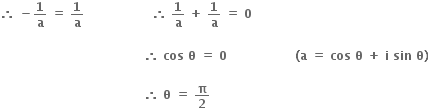
હવે f(x) = 0 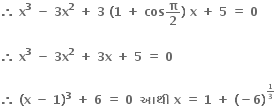
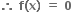 ને એક ઋણ વાસ્તવિક બીજ મળે.
ને એક ઋણ વાસ્તવિક બીજ મળે.
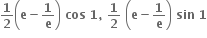
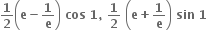
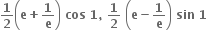
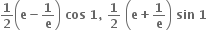
24, 7
25, 19
31, 29
31, 19
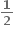 હોય, તો જેના બીજ (α + iβ)100 અને (α - iβ)100 હોય તેવું સમીકરણ .......
હોય, તો જેના બીજ (α + iβ)100 અને (α - iβ)100 હોય તેવું સમીકરણ ....... x2 + x - 1 = 0
x2 - x - 1 = 0
x2 - x + 1 = 0
x2 + x + 1 = 0
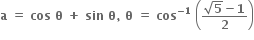
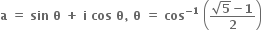
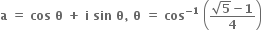
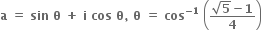
1
2n
2n-1
3n-1
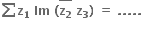
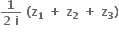
0

1
-1
2
0