CBSE
 Multiple Choice Questions
Multiple Choice Questions
P-i, Q-ii, R-iii, S-iv
P-ii, Q-ii, R-iv, S-iii
P-iv, Q-iii, R-ii, S-i
P-iv, Q-i, R-ii, S-iii
(x-1)એ P(x) તથા Q(x) બંનેનો અવયવ હોય.


P-1, Q-2, R-4, S-3
P-2, Q-1, R-3, S-4
P-2, Q-1, R-4, S-3
P-1, Q-2, R-3, S-4
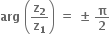
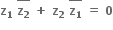
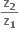 એ વાસ્તવિક સંખ્યા હોય.
એ વાસ્તવિક સંખ્યા હોય.
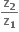 એ શુદ્વ કાલ્પનિક સંખ્યા છે.
એ શુદ્વ કાલ્પનિક સંખ્યા છે.
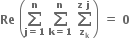 હોય તો,
હોય તો,
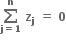
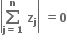
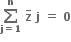

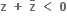
A.

B.
z એ x+y+1 = 0 પર છે.C.
|z| એ x2 + y2 + 2x - 4y - 8 = 0 ની ત્રિજ્યા છે.D.
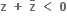
Tips: -
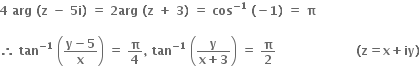
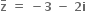

 = -6 < 0
= -6 < 0
P-ii, Q-iii, R-i, S-iv
P-i, Q-ii, R-iii, S-iv
P-iv, Q-iii, R-ii, S-i
P-ii, Q-i, R-iv, S-iiii
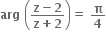 તો |z-2i| ની કિંમત = ......
તો |z-2i| ની કિંમત = ......
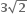

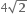
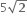

P-iii, Q-ii, R-iv, S-i
P-i, Q-ii, R-iii, S-iv
P-ii, Q-iii, R-iv, S-i
P-iv, Q-iii, R-ii, S-i