CBSE
 Multiple Choice Questions
Multiple Choice Questions = .......... rad
= .......... rad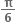 (ii)
(ii)  (iii)
(iii) 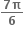 (iv)
(iv) 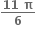
 (ii)
(ii)  (iii)
(iii)  (iv)
(iv) 
1 (ii) 2 (ii) 3 (i) 4 (iii)
1 (i) 2 )ii) 3 (iii) 4 (iv)
1 (ii) 2 (ii) 3 (iv) 4 (iv)
1 (ii) 2 (ii) 3 (iii) 4 (iv)
વિધાન : ડોપ્લર અસરમાં ધ્વનિ-ઉદ્દગમના આગળના વિસ્તારમાં તરંગોની તરંગલંબાઈ ઘટે છે, જ્યારે પાછળના વિસ્તારમાં તરંગલંબાઈ વધે છે.
કારણ : તરંગ અને ધ્વનિ ઉદ્દ્ગમ વચ્ચે સાપેક્ષ સ્થાનાંતર હોય છે.
વિધાન અને કારણ બંને સાચાં છે તથા કારણ એ વિધાનનું સમર્થન કરે છે.
વિધાન અને કારણ બંને સાચાં છે પરંતુ કારણ એ વિધાનનું સમર્થન કરતું નથી.
વિધાન સાચું છે પરંતુ કારણ ખોટું છે.
વિધાન ખોટું છે પરંતુ કારણ સાચું છે.
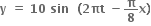 છે. જ્યાં y અને x cm માં અને t s માં છે, તો નીચેના પ્રશ્નોના જવબો આપો :
છે. જ્યાં y અને x cm માં અને t s માં છે, તો નીચેના પ્રશ્નોના જવબો આપો :  (iii) 20
(iii) 20  (iv) 30
(iv) 30 
 (iii) 40
(iii) 40  (iv) -40
(iv) -40 
1 (iii) 2 (ii) 3 (iii) 4 (i)
1 (iii) 2 (i) 3 (iii) 4 (iv)
1 (ii) 2 (iii) 3 (iv) 4 (iv)
1 (ii) 2 (ii) 3 (ii) 4 (i)
 છે.)
છે.)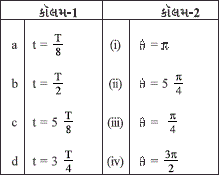
a (iii) b (i) c (iv) d (ii)
a (ii) (b) (iii) c (i) d (iv)
a (iv) b (i) c (ii) d (iii)
a (iii) b (i) c (ii) d (iv)

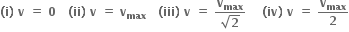
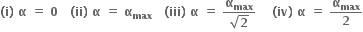

1 (ii) 2 (iii) 3 (iii) 4 (ii)
1 (ii) 2 (iv) 3 (iii) 4 (iii)
1 (i) 2 (ii) 3 (i) 4 v(iii)
1 (ii) 2 (iii) 3 (iii) 4 (iv)
A.
1 (ii) 2 (iii) 3 (iii) 4 (ii)
વિધાન : ક્લોઝડ પાઈપ માટે fn એ (n-1)મો ઓવરસ્ટોન દર્શાવે છે.
કારણ : ક્લોઝડ પાઈપ માટે બધા જ હાર્મોનિક શક્ય છે.
વિધાન અને કારણ બંને સાચાં છે તથા કારણ એ વિધાનનું સમર્થન કરે છે.
વિધાન અને કારણ બંને સાચાં છે પરંતુ કારણ એ વિધાનનું સમર્થન કરતું નથી.
વિધાન સાચું છે પરંતુ કારણ ખોટું છે.
વિધાન ખોટું છે પરંતુ કારણ સાચું છે.
 છે. જ્યાં x અને y cm માં અને t s માં છે તો,
છે. જ્યાં x અને y cm માં અને t s માં છે તો, 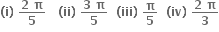
1 (i) 2 (ii) 3 (iii) 4 (iv)
1 (i) 2 (ii) 3 (iii) 4 (ii)
1 (i) 2 (iii) 3 (ii) 4 (ii)
1 (ii) 2 (ii) 3 (iii) 4 (iv)
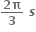 છે, તો નીચેના પ્રશ્નોના જવાબ આપો :
છે, તો નીચેના પ્રશ્નોના જવાબ આપો : 1 (i) 2 (i) 3 (i) 4 (i)
1 (iv) 2 (iv) 3 (iv) 4 (iv)
1 (iv) 2 (i) 3 (iv) 4 (i)
1 (iv) 2 (i) 3 (i) 4 (iv)
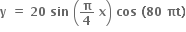 છે. જ્યાં x અને y cm અને t s માં છે, તો
છે. જ્યાં x અને y cm અને t s માં છે, તો 1 (i) 2 (iv) 3 (ii) 4 (iii)
1 (i) 2 (iv) 3 (iii) 4 (ii)
1 (i) 2 (i) 3 (iii) 4 (ii)
1 (iii) 2 (iii) 3 (ii) 4 (ii)
વિધન : સ્પંદની ઘટના એકમ સમયમાં ધ્વનિ 2 (f1 - f2) વખત મહત્તમ થાય છે.
કારણ : એકમ સમય દીઠ સ્પંદની સંખ્યા (f1 - f2) છે.
વિધાન અને કારણ બંને સાચાં છે તથા કારણ એ વિધાનનું સમર્થન કરે છે.
વિધાન અને કારણ બંને સાચાં છે પરંતુ કારણ એ વિધાનનું સમર્થન કરતું નથી.
વિધાન સાચું છે પરંતુ કારણ ખોટું છે.
વિધાન ખોટું છે પરંતુ કારણ સાચું છે.