CBSE
Class 10 Class 12
The change in direction of light when it passes from one medium to another obliquely is called refraction of light, or the bending of light when it goes from one medium to another obliquely is called refraction of light.
Some examples of refraction :
The refraction takes place when light enters from rarer to the denser medium or vice versa. The speed of light is different in different substances. The refraction of light is due to the change in the speed of light on going from one medium to another.
The speed of light is maximum in a vacuum is 3 × 108 m/s.
A transparent substance in which light travels is known as a medium. The medium can be divided into two types:
The glass is an optically denser medium than air and water.
The type of image formed by a convex lens depends on the position of the object in front of the lens. There are six positions of the object:
Nature, position and relative size of the image formed by a convex lens for various positions of the object
| position of the object | Position of Image | Size of the Image | Nature of Image |
| At infinity | At the focus F2 | Highly diminished,point-sized | Real and inverted |
| Beyond 2F1 | Between F2 and 2F2 | Diminished | Real and inverted |
| At 2F1 | At 2F2 | Same size | Real and inverted |
| Between F1 and 2F1 | Beyond 2F2 | Enlarged | Real and inverted |
| At F1 | At infinity | Highly enlarged | Real and inverted |
| Between F1 and optical centre O | Behind the mirror | Enlarged | Virtual and erect |
Nature, position and relative size of the image formed by a concave lens for various positions of the object
| Position of object | Position of Image | Size of Image | Nature of Image |
| At infinity | At the focus F1 | Highly diminished,point-sized | Virtual and erect |
| Between infinity and the optical centre O of the Lens | Between O and F1 behind the mirror | Diminished | Virtual and erect |
Convex Lens image formation:

Concave lens image formation:

Lens formula gives the relationship between object distance (u), image-distance (v) and the focal length (f ). The lens formula is expressed as,

where ‘u’ is the distance of the object from the optical centre (O), ‘v’ is the distance of the image from the optical centre (O) and ‘f’ is the distance of the principal focus from the optical centre (O).
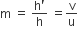
It is defined as the ratio of the height of the image and the height of the object.
It is represented by the letter m. If h is the height of the object and h’ is the height of the image given by a lens, then the magnification produced by the lens is given by,

Magnification produced by a lens is also related to the object-distance u, and the image-distance v. This relationship is given by
The power of a lens is defined as the reciprocal of its focal length. It is represented by the letter P. The power P of a lens of focal length f is given by
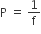
The SI unit of power of a lens is ‘dioptre’. It is denoted by the letter D.
If f is expressed in metres, then, power is expressed in dioptres. Thus, 1 dioptre is the power of a lens whose focal length is 1 metre. 1D = 1m–1
The power of a convex lens is positive and that of a concave lens is negative.
A lens is any transparent material (e.g. glass) of an appropriate shape that can take parallel rays of incident light and either converge the rays to a point or diverge the rays from a point.
Convex lens: A lens may have two spherical surfaces, bulging outwards. Such a lens is called a double convex lens. It is simply called a convex lens. Convex lens converges light rays. Hence it is called a converging lens.
Concave lens: A double concave lens is bounded by two spherical surfaces, curved inwards. concave lens diverges light rays and is called diverging lenses. A double concave lens is simply called a concave lens.
Important Terms:
Principal Axis: An imaginary straight line passing through the two centres of the curvature of a lens is called its principal axis.
Optical Centre: The optical centre (O) of a convex lens is usually the centre point of the lens. The direction of all light rays which pass through the optical centre remains unchanged.
Centre of Curvature: A lens has two spherical surfaces. Each of these surfaces forms a part of a sphere. The centres of these spheres are called centres of curvature of the lens. The centre of curvature of a lens is usually represented by the letter C. Since there are two centre’s of curvature, we may represent them as C1 and C2.
Aperture: The effective diameter of the circular outline of a spherical lens is called its aperture.
Focal Length: The focal length (f) is the distance between the optical centre and the focal point.

The extent of bending of a ray of light at the opposite parallel faces of rectangular glass slab is equal and opposite, so the ray emerges parallel to the incident ray.
Lateral displacement depends on :
The lens formula we must make use of proper sign convention while taking the values of an object (u), image distance (v), focal length (f), object height (h) and image height (h’). The sign conventions are as follows:

Consequences of new Cartesian sign convention:
Rules of refraction
Rule-1: When a light ray travels from a rarer medium to a denser medium, the light ray bends towards the normal.
Rule-2: When a light ray travels from a denser medium to a rarer medium, the light ray bends away from the normal.

According to laws of refraction of light.
The incident ray, the refracted ray and the normal to the interface of two transparent media at the point of incidence, all lie in the same plane.
The ratio of the sine of the angle of incidence to the sine of the angle of refraction is a constant, for the light of a given colour and for the given pair of media.This law is also known as Snell’s law of refraction.
If i is the angle of incidence and r is the angle of refraction, then,