CBSE
Class 10 Class 12

The total flux will be a combination of the faces 1 and 2 as other faces are parallel to the electric field.
Net flux = 2EA
charge enclosed by closed surface = σA
From Gauss's Law,
2 EA = σA/ε0
or, E = σ/2ε0
Vectorically,

The total flux will be a combination of the faces 1 and 2 as other faces are parallel to the electric field.
Net flux = 2EA
charge enclosed by closed surface = σA
From Gauss's Law,
2 EA = σA/ε0
or, E = σ/2ε0
Vectorically,
σ be the uniform surface charge density of a thin spherical shell of radius R. The field at any point P, outside or inside, can depend only on r (the radial
distance from the centre of the shell to the point) and must be radial (i.e., along with the radius vector).

Due to spherical symmetry, the electric field at each point of the Gaussian surface has the same magnitude.
E and ΔS at every point are parallel and the flux through each element is EΔS.
The Gaussian surface is E × 4πr2.The charge enclosed is σ ×4πR2 . By Gauss’s law
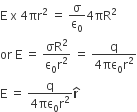
where q = 4πR2σ is the total charge on the spherical shell.
The electric field is directed outward if q > 0 and inward if q < 0.
The point P is inside the shell. The Gaussian surface is again a sphere through P centred at O.

Due to spherical symmetry, the electric field at each point of the Gaussian surface has the same magnitude.
E and ΔS at every point are parallel and the flux through each element is EΔS.
Net flux = charge enclosed
or
E × 4πr2= 0
i.e., E = 0 (r < R ) that is, the field due to a uniformly charged thin shell is zero at all points inside the shell.
Flux through the Gaussian surface
= flux through the curved cylindrical part of the surface
= E × 2πrl
The surface includes charge equal to λ l. Gauss’s law then gives
E × 2πrl = λl/ε0
i.e., E = λ/ 2πε0r
vectorially, E at any point is given by
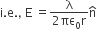
where nˆ is the radial unit vector in the plane normal to the wire passing through the point.