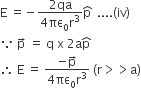Electric Charges and Fields

Quickly browse through questions and notes on related topics. You can also download and read this topic offline.

• Questions
• Summary

A uniform electric field has constant magnitude and fixed direction. Such a field is produced between the plates of a charged parallel plate capacitor.

When two charges in a dipole are separated by some distance, the forces acting at different points result in a torque on the dipole.The torque tries to align the dipole with an electric field. Once aligned, the torque becomes 0.

Magnitude of torque

τ = qE x 2a sinθ
τ = 2qaE sinθ
τ = pEsinθ.

The vector form of torque is the cross product of dipole moment and electric field.

1. In most molecules, the centres of positive charges and of negative charges lie at the same place. Therefore, their dipole moment is zero. For example CO₂ and CH₄. However, they develop a dipole moment when an electric field is applied. 
2. In some molecules, the centres of negative charges and of positive charges do not coincide. Therefore they have a permanent electric dipole moment, even in the absence of an electric field. Such molecules are called polar molecules. For example H₂O.

The magnitudes of the electric field due to the two charges +q and -q are given by,

The directions of E+q and E-q are as shown in the figure. The components normal to the dipole axis cancel away. The components along the dipole axis add up.
Therefore, Total electric field.

E = - (E+q + E-q) cosθ p [Negative sign shows that field is opposite to p]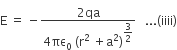

At large distances (r>>a),this reduces to