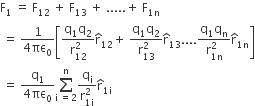CBSE
Class 10 Class 12
consider a system of three charges q1, q2 and q3, as shown in given figure.The force on one charge, say q1, due to two other charges q2, q3 can, therefore, be obtained by
performing a vector addition of the forces due to each one of these charges. Thus, if the force on q1 due to q2 is denoted by F12, F12 is given by,


In the same way, the force on q1 due to q3, denoted by F13, is given by
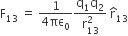
which again is the Coulomb force on q1 due to q3, even though other charge q2 is present.
The principle of superposition says that in a system of charges q1, q2, ..., qn, the force on q1 due to q2 is the same as given by Coulomb’s law, i.e., it is unaffected by the presence of the other charges q3, q4, ..., qn. The total force F1 on the charge q1, due to all other charges, is then given by the vector sum of the forces F12, F13, ..., F1n: