81. State and explain Charle’s law.

Charle's law states:  Pressure remaining constant the volume of a given mass of gas increases or decreases by  volume at  for each one-degree rise or fall in temperature. 
Mathematically,
 If V₀ is the volume at 0°C, then the volume at various other temperatures can be written as:
     
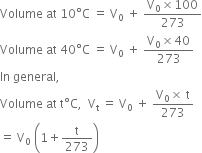
But if the gas is cooled to –273°C, then its volume becomes zero.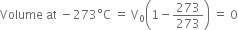

This implies that a gas at -273°C will have zero or no volume i.e. it will cease to exist. In actual practice, all gases liquefy before this temperature is reached. Also –273°C should be the lowest possible temperature because any further cooling would lead to a volume of less than zero or negative volume which is meaningless. Therefore, this temperature (–273° C) was termed as absolute zero of temperature.
Another statement of Charle’s law:
According to Charle’s law, volume of a given mass of a gas at different temperatures is related to its volume (V₀) at 0°C as follows:
Volume at 



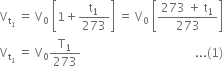
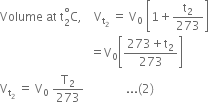
Dividing (1) by (2), we get,
     
 

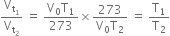
[Pressure and mass of the gas constant]
Hence Charle’s law may also be stated as Pressure remaining constant, the volume of a given mass of a gas is directly proportional to absolute temperature i.e. 
Thus, if V₁ is the initial volume of the gas at temperature T₁ (in degree kelvin) and V₂ is the final volume of the gas at temperature T₂ (in degree kelvin), keeping pressure constant, then