Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Application of Derivatives

Name: Zigya - For The Curious Learner
Rating: 4.4 (740 reviews)

Short Answer Type

21. The surface area of a spherical bubble is increasing at the rate of 2 cm²/sec. Find the rate at which the volume of the bubble is increasing at the instant its radius is 6 cm.

223 Views

22.

The volume of a spherical balloon is increasing at the rate of 25 cm³/sec. Find the rate of change of its surface area at the instant when its radius is 5 cm.

87 Views

Long Answer Type

23. The radius of a spherical soap bubble is increasing at the rate of 0.3 cms^–1. Find the rate of change of its (i) volume (ii) surface area when the radius is 8 cm.

203 Views

24. The radius of a spherical soap bubble is increasing at the rate of 0.2 cms^–1. Find the rate of change of its (i) volume (ii) surface area, when the radius is 4 cm.

105 Views

25. The radius of a spherical soap bubble is increasing at the rate of 0.4 cms^–1 Find the rate of change of its (i) volume (ii) surface area, when the radius is 10 cm.

88 Views

Short Answer Type

26.

A ballon which always remains spherical on inflation, is being inflated by pumping in 900 cubic centimetres of gas per second. Find the rate of which the radius of the balloon is increasing when the radius is 15 cm.

93 Views

27.

The volume of a cube is increasing at a rate of 9 cubic centimeters per second. How fast is the surface area increasing when the length of an edge is 10 centimeters?

102 Views

28.

The volume of a cube is increasing at a rate of 7 cubic centimeters per second. How fast is the surface area increasing when the length of an edge is 12 centimeters?

74 Views

29. The volume of a cube is increasing at the rate of 8 cm³/s. How fast is the surface area increasing when the length of an edge is 12 cm?

Let V be volume of cube of side x.

therefore space space space space space space space space space space space space space straight V space equals space straight x cubed

From given condition,

dV over dt space equals space 8 space cm cubed divided by straight s

therefore space space space space straight d over dt left parenthesis straight x cubed right parenthesis space equals space 8 space space space space space space space space space space space space rightwards double arrow space space space space 3 straight x squared dx over dt space equals space 8 space space space rightwards double arrow space space space space dx over dt space equals fraction numerator 8 over denominator 3 straight x squared end fraction space space space space space space space space space space space space space... left parenthesis 1 right parenthesis

Let S be surface area of cube

therefore space space space space space straight S space equals space 6 straight x squared

Rate of increase of surface area =

dS over dt space equals space straight d over dt left parenthesis 6 straight x squared right parenthesis

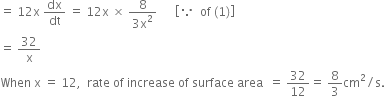
equals space 12 straight x space dx over dt space equals space 12 straight x space cross times space fraction numerator 8 over denominator 3 straight x squared end fraction space space space space space space open square brackets because space space of space left parenthesis 1 right parenthesis close square brackets equals space 32 over straight x When space straight x space equals space 12 comma space space rate space of space increase space of space surface space area space space equals space 32 over 12 equals space 8 over 3 cm squared divided by straight s.

105 Views

30.

The length x of a rectangle is decreasing at the rate of 2 cm/s and the width y is increasing at the rate of 2 cm/s. When x = 12 cm and y = 5 cm, find the rate of change of (a) the perimeter and (b) the area of the rectangle.

139 Views