41. A point source of light along a straight road is at a height of ‘a’ metres. A boy ‘b’ metres in height is walking along the road. How fast is his shadow increasing if he is walking away from the light at the rate of c metres per minute?

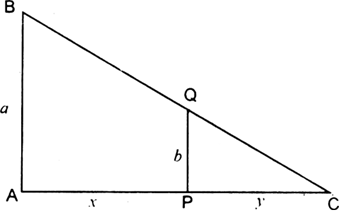
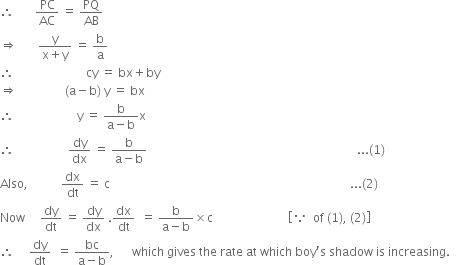
Water is dripping out from a conical funnel, at the uniform rate of 2 cc/sec through a tiny hole at the vertex of the funnel. When the slant height of water is 5 cm, find the rate of decrease of the slant height of the water.

An inverted cone has a depth of 10 cm and a base of radius 5 cm. Water is poured into it at the rate of  Find the rate at which the level of water in the cone is rising when the depth is 4 cm.

The total revenue in Rupees received from the sale of x units of a product is given by R(x) = 3x ² + 36x + 5.

• 116

• 96

• 90

• 90

A cylindrical tank of radius 10 m is being filled with wheat at the rate of 314 cubic metre per hour. Then the depth of the wheat is increasing at the rate of 

• 1 m³/h

• 0 · 1 m³/h
• 1 · 1 m³/h
• 1 · 1 m³/h

Show that the tangent to the curve y = 7x³ + 11 at the points where x = 2 and x = – 2 are parallel.