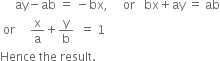Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type Short Answer Type
Short Answer Type Long Answer Type
Long Answer TypeProve that the line ![]() is a tangent to the curve
is a tangent to the curve ![]() at the point where the curve cuts y-axis.
at the point where the curve cuts y-axis.
The equation of given curve is ![]() ...(1)
...(1)
It cuts y-axis where x = 0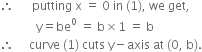
Differentiating (1), w.r.t. x, we get,
![]()
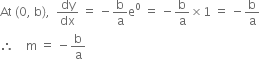
The equation of tangent (0, b) with ![]()
![]()
![]()