101. Find the point on the curve y = x³ – 11 x + 5 at which the tangent has the equation y = x – 11.

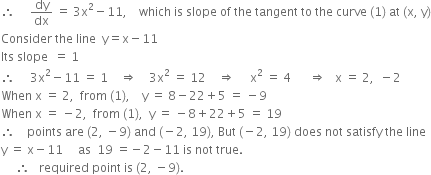
Find the point on the curve y = x³ – 2x² – 2x at which the tangent lines are parallel to the line y = 2x – 3.

Find the points on the curve y = x³ – 2x² – x at which the tangent lines are parallel to the line y = 3x – 2.

Find the equation of the tangent to the curve x² + 3y = 3, which is parallel to the line y – 4x + 5 = 0. 

Find the equations of all lines having slope -1 that are tangents to the curve  

Find the equation of all lines having slope 2 and being tangent to the curve .

Find the equation of all lines having 0 slope and that are tangent to the curve 

Find the equation of the tangent to the curve  which is parallel to the line 4x - 2y + 5 = 0

Find the equation of tangents to the curve
y = cos (x + y), – 2  ≤ x ≤ 2 
that are parallel to the line x + 2y = 0.

Find the point on curve 4x² + 9y² = 1, where the tangents are perpendicular to the line 2y + x = 0.