 Short Answer Type
Short Answer TypeFind points on the curve ![]() at which the tangents are (i) parallel to the x-axis (ii) parallel to the y-axis.
at which the tangents are (i) parallel to the x-axis (ii) parallel to the y-axis.
 Long Answer Type
Long Answer TypeFind points on the curve ![]() at which the tangents are (i) parallel to the x-axis (ii) parallel to the y-axis.
at which the tangents are (i) parallel to the x-axis (ii) parallel to the y-axis.
For the curve y = 4x3 – 2x5, find all the points at which the tangent passes through the origin.
 Multiple Choice Questions
Multiple Choice Questions Long Answer Type
Long Answer TypeShow that the curves 2x = y2 and 2xy = k cut at right angles if k2 = 8
The equation of two curves are
2x = y2 ...(1)
and ![]() ...(2)
...(2)
From (1) and (2), ![]()
![]()
![]() point of intersection of curves (1) and (2) is
point of intersection of curves (1) and (2) is ![]()
From (1), ![]()
![]()
![]()
From (2), ![]()
At 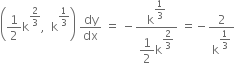
![]()
Curves (1) and (2) cut at right angles if ![]()
i.e., if ![]()
i.e. if ![]()
Hence the result.
If the curve αx2 + βy2 = 1 and α' x2 + β'y2 = 1 intersect orthogonally, prove that (α – α') β β') = (β – β') α α'.
 Multiple Choice Questions
Multiple Choice Questions