 Short Answer Type
Short Answer TypeFind points on the curve ![]() at which the tangents are (i) parallel to the x-axis (ii) parallel to the y-axis.
at which the tangents are (i) parallel to the x-axis (ii) parallel to the y-axis.
 Long Answer Type
Long Answer TypeFind points on the curve ![]() at which the tangents are (i) parallel to the x-axis (ii) parallel to the y-axis.
at which the tangents are (i) parallel to the x-axis (ii) parallel to the y-axis.
For the curve y = 4x3 – 2x5, find all the points at which the tangent passes through the origin.
 Multiple Choice Questions
Multiple Choice Questions Long Answer Type
Long Answer TypeIf the curve αx2 + βy2 = 1 and α' x2 + β'y2 = 1 intersect orthogonally, prove that (α – α') β β') = (β – β') α α'.
The equations of two curves are
![]() ...(1)
...(1)
and ![]() ...(2)
...(2)
Let curves (1) and (2) intersect at ![]()
![]() ...(3)
...(3)
and ![]() ...(4)
...(4)
Subtracting (4) from (3), we get,
![]()
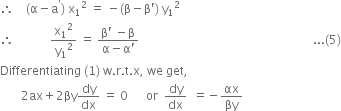
At ![]()
Similarly for second curve,
![]()
Since the two curves (1) and (2) intersect orthogonally,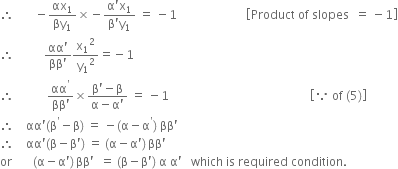
 Multiple Choice Questions
Multiple Choice Questions