141.

Show that the function given by f(x) = e^2x is strictly increasing on R.

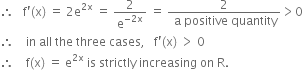
Prove that f (x) = ax + b, where a and b are constants and a > 0 is an strictly increasing function for all real values of x. without using the derivative.

Prove that the logarithmic function is increasing wherever it is defined.

Show that the function f given by f (x) = 10^x is increasing for all x.

Prove that the function f(x) = x³ – 3x² + 3x – 100 is increasing on R.

Prove that the function f(x) = x³ – 3x² + 3x – 100 is increasing on R.

Prove that the function f (x) = sinx is
(i) strictly increasing in 
(ii) strictly decreasing in 
(iii) neither increasing nor decreasing in .

Prove that the function f (x) = cos x is
(i) strictly increasing in 
(ii) strictly decreasing in 
(iii) neither increasing nor decreasing in