 Long Answer Type
Long Answer TypeProve that ![]() is an increasing function of
is an increasing function of ![]() in
in ![]() .
.
Here, ![]()
![]()
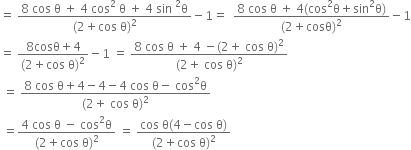
For y to be increasing, ![]()
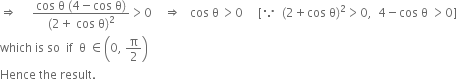
Find the intervals in which the function f is given by
![]()
is (i) increasing (ii) decreasing
Determine the values of x for which the function ![]() is increasing and for which it is decreasing.
is increasing and for which it is decreasing.
 Short Answer Type
Short Answer TypeLet I be any interval disjoint from (– 1, 1). Prove that the function f given by ![]() is strictly increasing on I.
is strictly increasing on I.
Find the intervals in which the function f given by f(x) = 2x2 – 3x is
(a) strictly increasing (b) strictly decreasing
Find the intervals in which the function f given by f(x) = x2 – 4x+6 is
(a) strictly increasing (b) strictly decreasing
Find the intervals in which the following functions are strictly increasing or decreasing:
x2+ 2x – 5
Find the intervals in which the following functions are strictly increasing or decreasing:
10 – 6x – 2x2
