 Short Answer Type
Short Answer TypeFind the intervals in which the following functions are strictly increasing or strictly decreasing:
2x3 – 8x2 + 10x + 5
Find the intervals in which the following functions are strictly increasing or strictly decreasing:
2x3 – 6x2 – 48x + 17
Find the intervals in which the following functions are strictly increasing or strictly decreasing:
f (x) = 2x3 – 9x2 + 12x + 30
Find the intervals in which the following functions are strictly increasing or strictly decreasing:
f (x) = 2x3 – 3x2 – 36x + 7
Find the intervals in which the following functions are strictly increasing or strictly decreasing:
f(x) = 2x3 – 21x2 + 36x – 40
Find the intervals in which the following functions are strictly increasing or strictly decreasing:
4x3 – 6x2 – 72x + 30
Find the intervals in which the following functions are strictly increasing or strictly decreasing:
– 2x3 – 9x2 – 12x + 1
 Long Answer Type
Long Answer TypeFind the intervals in which the function f is given by ![]()
(i) increasing (ii) decreasing
Here ![]()
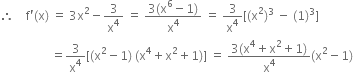
(i) For ![]() to be increasing
to be increasing
![]()
![]()
![]()
![]()
(ii) For f(x) to be decreasing,
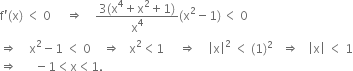
Determine for which values of x, the function f (x) = x4 – 2x2 is increasing or decreasing.
