 Long Answer Type
Long Answer TypeFind intervals in which the function given by ![]()
is (a) strictly increasing (b) strictly decreasing.
 Short Answer Type
Short Answer TypeFind the intervals in which the function ![]() is increasing or decreasing.
is increasing or decreasing.
Here, ![]()
![]()
(i) For f(x) to be increasing, ![]()
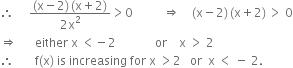
(ii) For f(x) to be decreasing, ![]()
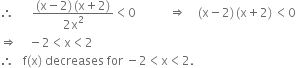
Separate ![]() into sub-intervals in which the function f (x) = sin 3x is increasing or decreasing.
into sub-intervals in which the function f (x) = sin 3x is increasing or decreasing.
 Long Answer Type
Long Answer TypeFind the intervals in which the following function is increasing or decreasing:
f (x) = sinx – cosx, 0 < x < 2![]() .
.
 Short Answer Type
Short Answer TypeFind the intervals in which the following function is increasing or decreasing
f (x) = (x + 2) e–x
 Long Answer Type
Long Answer TypeFind the intervals in which the function (x + 1)3 (x – 1)3 is strictly increasing or decreasing.
 Short Answer Type
Short Answer TypeLet f be a function defined on [a, b] such that f ' (x) > 0, for all x ∊ (a, b). Then prove that f is strictly increasing function of (a, b).
On which of the following intervals is the function f given by f (x) = x100 + sin x – 1 strictly decreasing?
(A) (0, 1) (B) ![]() (C)
(C) ![]() (D) None of these
(D) None of these
