Short Answer TypeFind the absolute maximum value and the absolute minimum value of the following functions in the given intervals:
Long Answer TypeFind the absolute maximum and minimum values of the function f given by
f (x) = cos2x + sinx, x ∊ [0, 
].
Find the points at which the function f given by f (x) = (x – 2)4 (x + 1 )3 has
(i) local maxima (ii) local minima (iii) point of inflexion .
Here, 
When x < 2 slightly, 
When x > 2 slightly, 
When x < -1 slightly f ' (x) = (-) (+) (-) = +ve
When x > -1 slightly, f ' (x) = (-) (+) (-) = +ve
at x = -1, f ' (x) does not change sign
x = -1 is a point of inflexion.
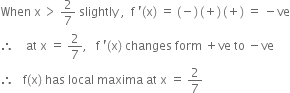
Short Answer TypeFind the local maxima or local minima, if any, of following functions using the first derivative test only. Find also the local maximum and the local minimum values, as the case may be:
The constant function 
Find the local maxima or local minima, if any, of following functions using the first derivative test only. Find also the local maximum and the local minimum values, as the case may be:
f(x) = x2
Find the local maxima or local minima, if any, of following functions using the first derivative test only. Find also the local maximum and the local minimum values, as the case may be:
Find the local maxima or local minima, if any, of following functions using the first derivative test only. Find also the local maximum and the local minimum values, as the case may be:
Find the local maxima or local minima, if any, of following functions using the first derivative test only. Find also the local maximum and the local minimum values, as the case may be:
Switch
