Long Answer TypeFind the area bounded by the curve y = x2 and the line y = x.
OR
Find the area of the region {(x. y): x2 ≤ y ≤ x}.
The given curve is
|x| + |y| = 1
or ± x ± y = 1
The given equation represents four lines
x + y = 1, x - y = 1,
- x + y = 1 and -x - y = 1
which enclose a square of diagonal 2 units length.
Required area is symmetrical in all the four quadrants.
∴ required area = 4 (area OAB)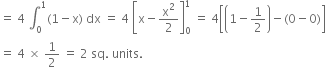
Find the area of the region bounded by the line y = 3 x + 2, the x-axis and the ordinates x = - 1 and x = 1.
Find the area of the region enclosed by the parabola x2 = y, the line y = x + 2 and the x-axis.
OR
Draw the rough sketch and find the area of the region:
{(x, y): x2 < y < x + 2}
Short Answer TypeDraw a rough sketch of the curves y = sin x and y = cos x as x varies from 0 to 
and find the area of the region enclosed by them and the x-axis.
Switch
.
