Long Answer TypeFind the area bounded by the curve y = x2 and the line y = x.
OR
Find the area of the region {(x. y): x2 ≤ y ≤ x}.
Find the area of the region bounded by the line y = 3 x + 2, the x-axis and the ordinates x = - 1 and x = 1.
Find the area of the region enclosed by the parabola x2 = y, the line y = x + 2 and the x-axis.
OR
Draw the rough sketch and find the area of the region:
{(x, y): x2 < y < x + 2}
The equation of parabola is
x2 = y ...(1)
The equation of line is
y = x + 2 ...(2)
From (1) and (2), we get,
x2 = x + 2
∴ x2 - x - 2 = 0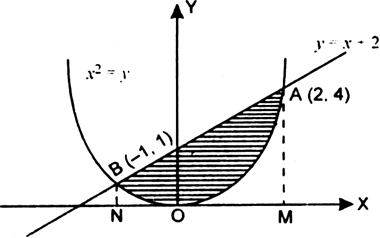
⇒ (x - 2) (x + 1) = 0 ⇒ x = 2, -1
∴ from (2), y= 2 + 2, -1 +2 = 4, 1
∴ parabola (1) meets line (2) in two points A (2, 4) and B (-1. 1).
From A. draw AM ⊥ x-axis and from B. draw BN ⊥ x-axis.
Required area = Area AOB
= 
Short Answer TypeDraw a rough sketch of the curves y = sin x and y = cos x as x varies from 0 to 
and find the area of the region enclosed by them and the x-axis.
Switch
.
